| Lecture
#23 |
| |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture Outline |
Quantum Theory of the Chemical Bond
Molecular Orbitals in Polyatomic Molecules
Molecular orbitals from combinations of hybrid
atomic orbitals
The rigid double bond
The freely rotating single sigma bond
Strained bonds
|
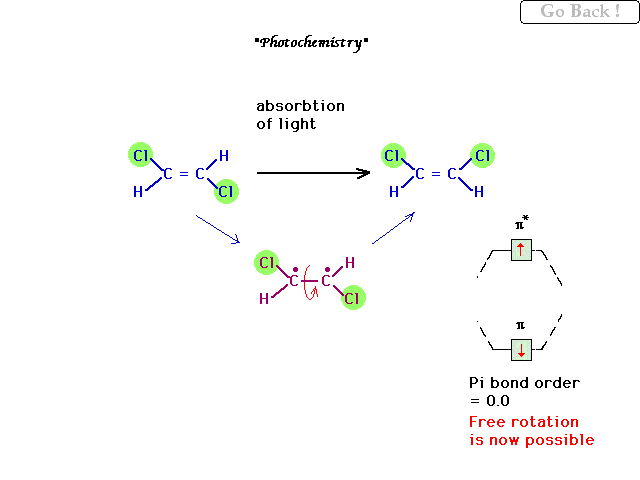
| A restricted rotation double bond can undergo a
"photochemical excitation" to an electronic
state in which the pi electrons revert to their atomic
orbitals owing to the cancelation of bonding vs
antibonding contributions. In this excited state, the CC
bond can now rotate briefly, while the excited molecule
lasts. |
 |
| Using a four-carbon system whose Lewis structure
indicates has two double bonds and one single bond, we
will show the molecular orbitals describing the pi
bonding are delocalized. |
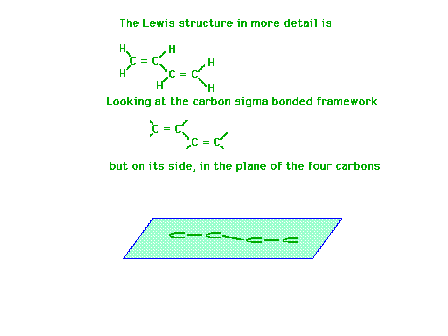 |
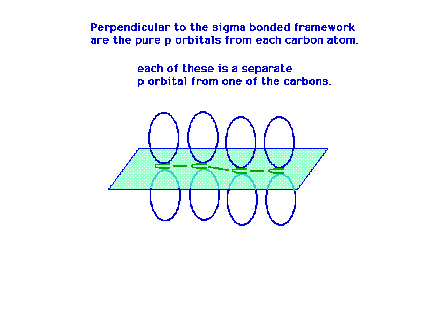
| Each carbon atom has a sigma framework involving sp2
orbitals leaving a pure 2p atomic orbital from which the
pi molecular orbital will arise. |
 |
| One of the linear combinations of the four atomic 2p
orbitals is entirely constructive -- in phase over all
four atoms -- and its resulting delocalized bonding
molecular orbital allows any electrons it contains to be
"spread" over the entire structure. |
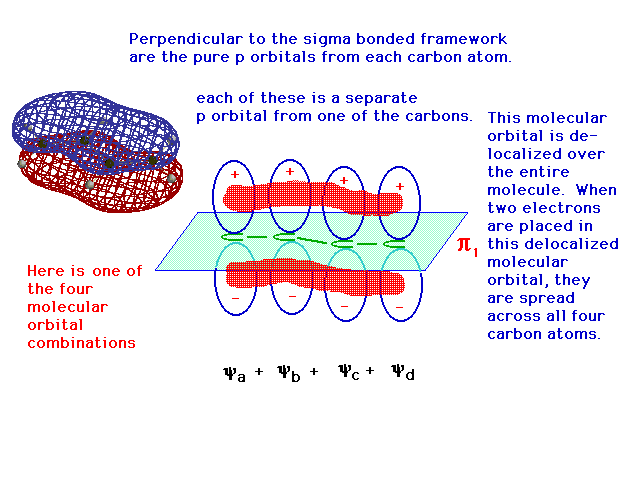 |
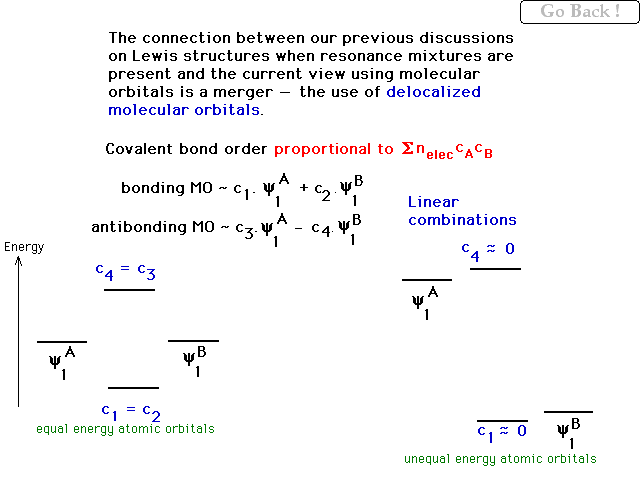
| The contribution of an overlap region to bond order
may be quantified with a simple relationship involving
the weighting coefficients "c" from the
combining atomic orbitals. For homonuclear diatomics, all
the c's are equal. For heteronuclear diatomic molecules,
in the bonding molecular orbital, c1 <<
c2 if c2 is the weighting factor of
the more electronegative species. |
 |
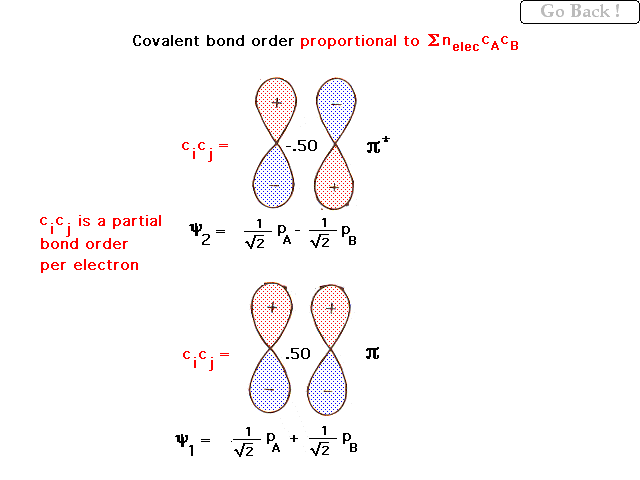
| This shows the equal contributions from 2p
orbitals in a homonuclear diatomic molecule. The actual
weighting coefficients are given (and will be provided,
their derivation being beyond what we need). The lower pi
bonding combination gives a "partial bond order per
electron" of 0.50 meaning two electrons in this
state (spin up and spin down) would give a bond order of
1.00 to the system. The antibonding partial bond order is
negative and exactly cancels the effect of an electron in
its bonding counterpart. |
 |
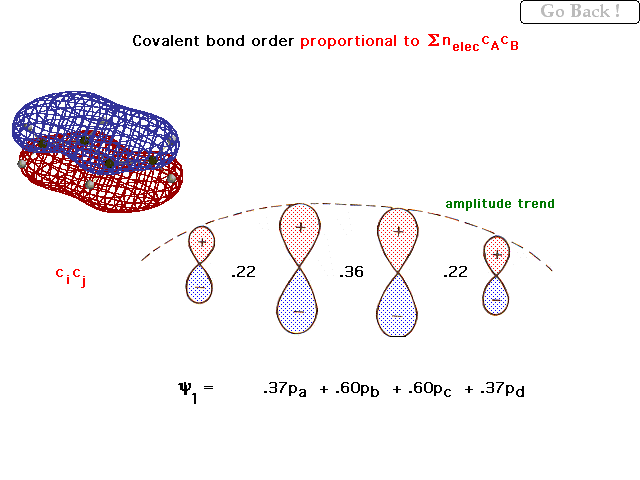
| For the 4 overlapping 2p orbitals in 1,3
butadiene, the weighting coefficients in the lowest,
bonding pi orbital are shown and these give rise to the
"bond order per electron" indicated between the
orbitals. The general trend in amplitudes (contributions)
is shown by the dashed line. |
 |
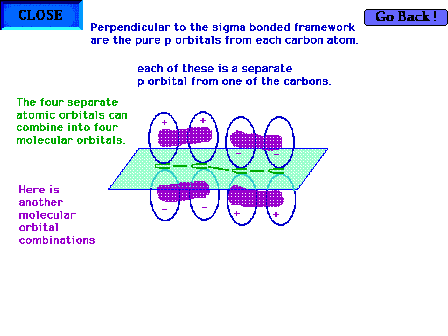
| Another of the four combinations of the four atomic
orbitals is shown here. This is also a bonding molecular
orbital. |
 |
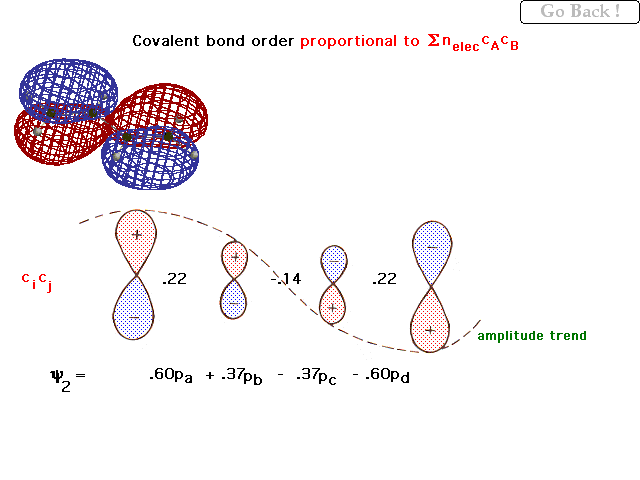
| The actual, quantitative "partial bond orders
per electron" and the weighting coefficients on the
next linear combination are given here (along with the
general trend as a dashed line). |
 |
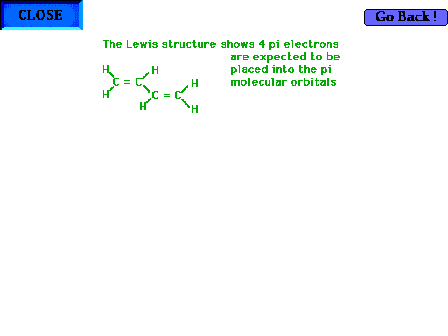
| A look at the original Lewis structure reminds us
that there are four pi electrons -- two from each of the
"double" part of the double bonds -- to be
distributed into the pi molecular orbitals. |
 |
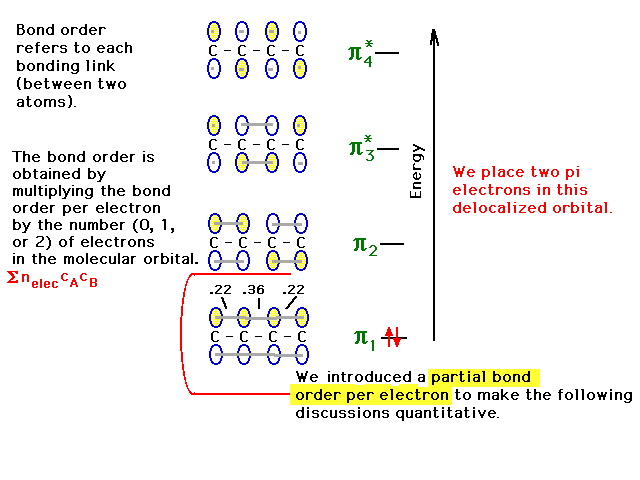
| Placing one of the pairs of pi electrons into the
lowest orbitals allows us to calculate the bond order due
to these electrons at each carbon-carbon link. We
introduce the idea of a partial bond order per
electron associated with each interatomic link for
each molecular orbital. Here, that partial bond order per
electron is half the result we got for the pair of
electrons or one-sixth for each CC link in pi orbital
#1.The bond order -- one-half the average number of
electrons per bond -- may be obtained from a given bond's
partial bond order per electron by multiplying
by the number of electrons in the orbital. Vice
versa, if you knew how the
electron(s) in a given molecular orbital were distributed
over the various links, you could get the partial
bond order per electron as we did for the lowest
pi-orbital. |
 |
| The remaining (second) pair of pi electrons goes into
the next state. We again calculate the bond order at each
carbon-carbon link due to these two electrons. The partial
bond order per electron is one-quarter for each of
the outer links and zero for the center CC link. |
 |
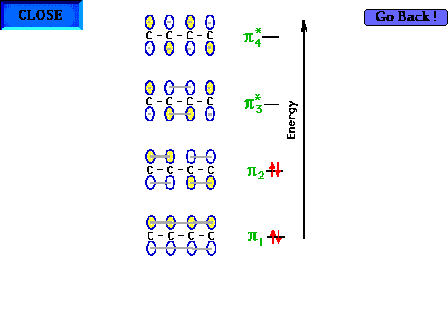
| The complete electron configuration for the four pi
electrons. |
 |
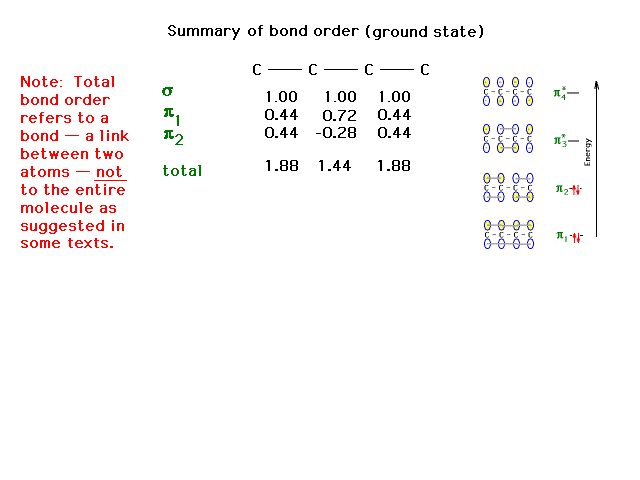
| The complete bond order for each carbon-carbon link
with contributions considered from the sigma and pi
molecular orbitals summed. |
 |
| The difference in the molecule's structure when
molecular orbital theory is used can be accommodated with
resonance Lewis structures that are not what we call
"preferred" structures, but which nevertheless
affect the overall appearance of the molecule. The bonds
are neither pure double bonds nor pure single bonds. |
 |
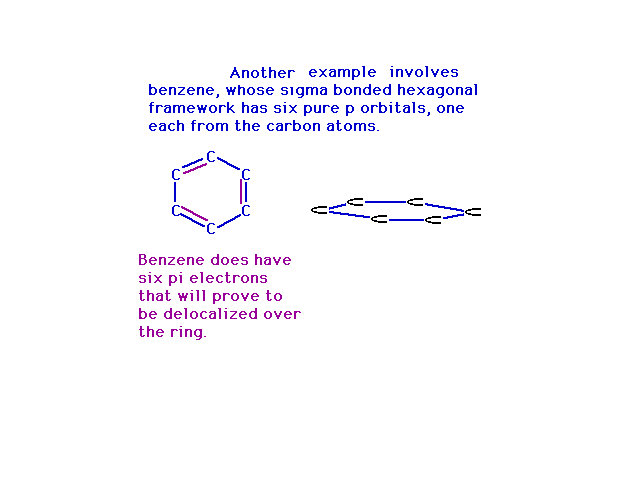
| Way back, when we were finishing up Lewis structures,
we used benzene as the prime example of where resonance
entered into play. In the molecular orbital view, the
resonance structures arise from place electrons into
delocalized orbitals constructed from various
combinations of atomic p orbitals. Note that steric
number three at each carbon gives us a trio of sp2 hybrid
atomic orbitals and a pure 2p atomic orbital
perpendicular to their plane. |
 |
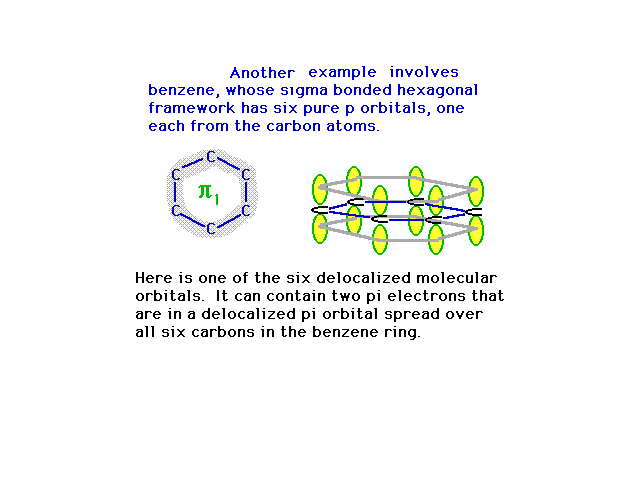
| The six 2p atomic orbitals are in position to overlap
in various ways, the most energetically stable being
constructive interference everywhere. This provides a
picture of the first pi molecular orbital. |
 |
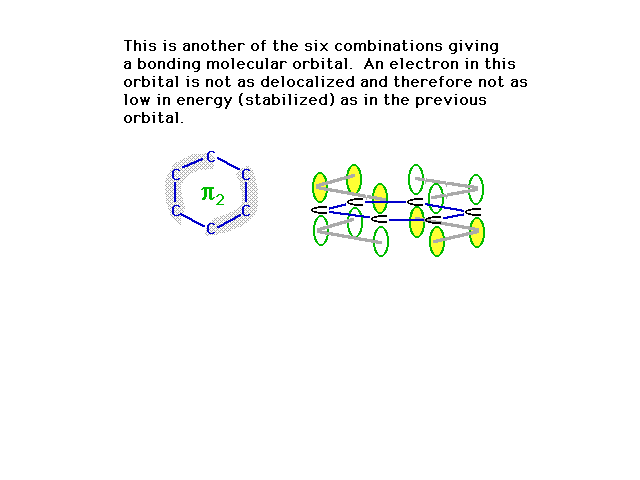
| A second combination is shown here in which a couple
of nodes are implied where the orbital amplitude switches
from + to -. |
 |
| The highest energy, least stable, molecular orbital
comes from the combination of atomic orbitals that has
the most destructive interference. Wave amplitude between
neighboring carbons is depleted in this combination which
is antibonding everywhere. |
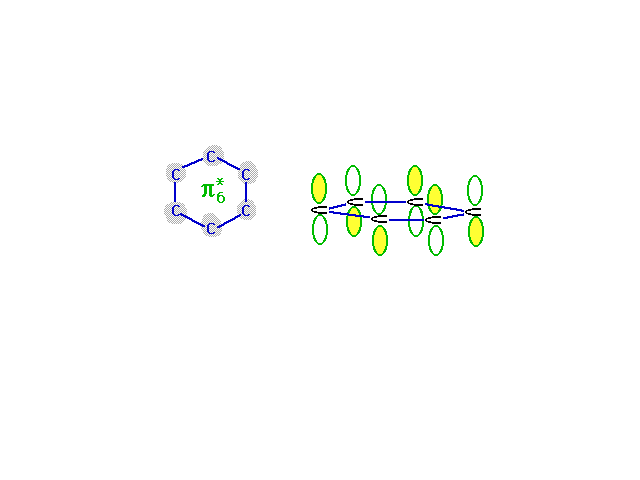 |
| The six combinations, some of which were not
illustrated, have energies indicated in this diagram. The
construction of the diagram is beyond this course, but
its use is straightforward since a total of six electrons
must be placed...as shown. |
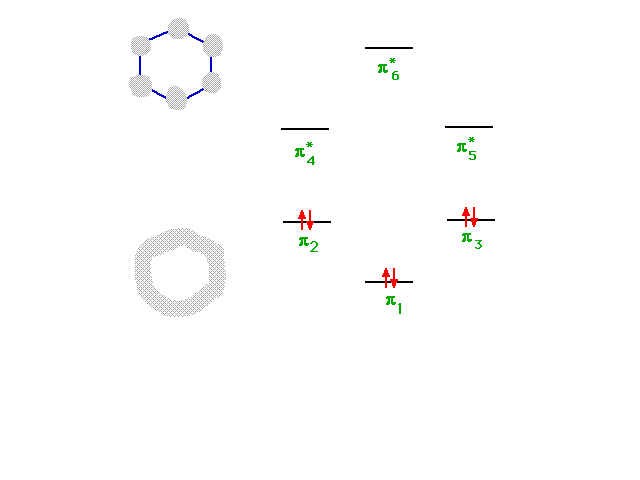 |




