| Lecture
#22 |
| Text: Section 14.1 |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture Outline |
Quantum Theory of the Chemical Bond
Molecular Orbitals
Polyatomic molecules
Hybrid atomic orbitals
|
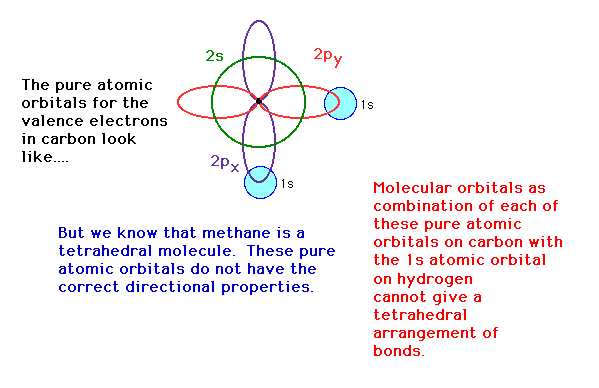
| Polyatomic molecues. In constructing a
picture for methane, the valence electron configuration
on carbon, 2s22p2 will not return
the correct directional properties for the bonds produced
by overlap with hydrogen's 1s atomic orbitals.
|
 |
| The 2s, 2px, 2py and 2pz
atomic orbital geometries are not tetrahedrally directed.
We need orbitals that have the correct directional
properties and we can synthesize these from our known
atomic orbitals by mixing, a process known here as hybridization.
We will look at an attempt at describing the bonding in
CH4. |
 |
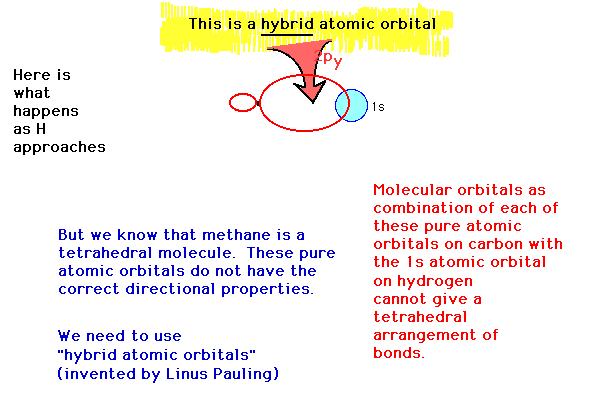
| A hybrid atomic orbital is an atomic
orbital obtained by combining two or more valence
orbitals on the same atom. |
 |
| In the CH4 molecule, we need two atomic
orbitals that are directed at 109.5 with respect to each
other, according to the "known" geometry.
(VSEPR tells us this.) Constructing hybrid orbitals from
the 2s and 2px atomic orbitals by taking
appropriate mixtures. These are being shown for
illustrative purposes. The math is not part of the
required material. "2s" represents the pure 2s
atomic orbital wave function, for example. The numerical
coefficients are not crucial to the demonstration. |
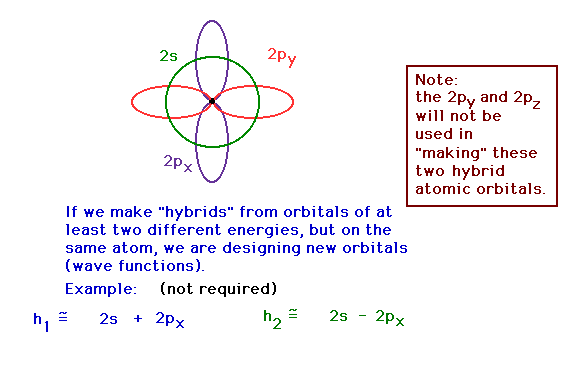 |
| Hybridizing from the 2s and 2px atomic
orbitals giving a hybrid orbital pointing in the
x-direction. This gives a hybrid that was just shown a
couple of slides earlier (in red). |
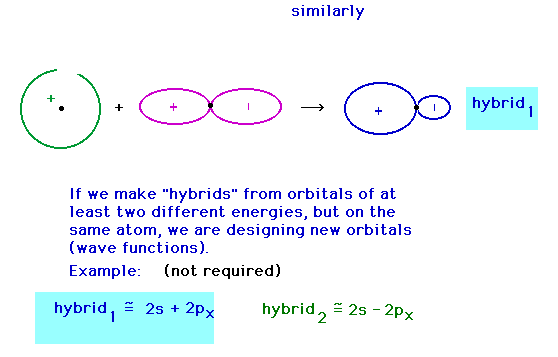 |
| Hybridizing from the 2s and 2px atomic
orbitals giving a hybrid pointing at 180o to
the previous hybrid. |
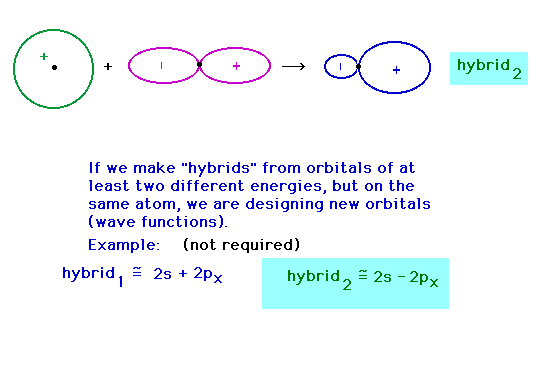 |
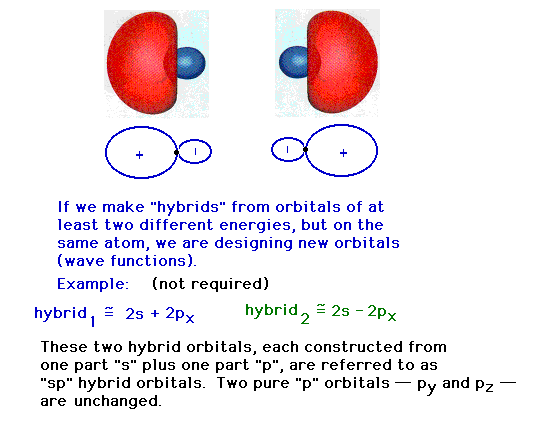
| The two pure atomic orbitals we have used have been
re-assembled into two mixed, hybrid atomic orbitals. Each
of the latter are identical in shape, but pointed in
different directions. The remaining 2p atomic orbitals
that have not been used remain unchanged in subsequent
discussions about the full set of valence atomic orbitals
in this system (that is, on the Be in beryllium hydride).
Now we return to a discussion of the atomic orbitals
that are appropriate to a tetrahedral geometry about a
central atom that had pure s and p atomic orbitals when
nothing else was around.
|
 |
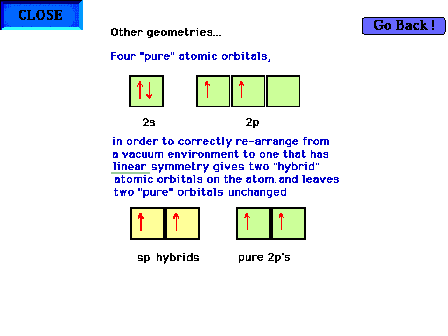
| Hybridization of s and p valence orbitals in a linear
environment (two perturbing
sites). Two of the orbitals,
the s and one of the p orbitals are mixed forming two sp hybrid orbitals, leaving
the remaining two p orbitals
as pure atomic orbitals. |
 |
| Hybridization of s and p valence orbitals in a
tetrahedral environment. That is, the carbon in this case
is surrounded by a tetrahedral arrangment of (four) objects (hydrogens) which
influence the behavior of carbons valence electrons. The
net result of all the forces (carbon at the center and a
tetrahedral arrangement of perturbations) gives four orbitals that are identical
in shape to each other and that are directed to the
vertices of a tetrahedron. These orbitals can be
simulated by hybridizing the four
previous pure orbitals through mixing mathematically and
are each symbolized as sp3 hybrid orbitals. |
 |
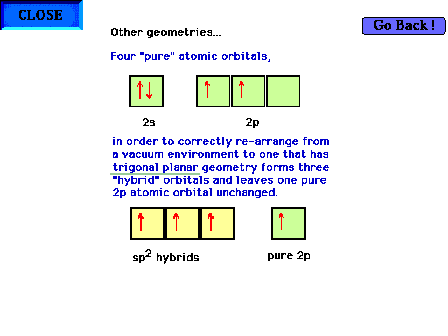
| Hybridization of s and p valence orbitals in a
trigonal planar environment (three
perturbing sites around the central atom). Three valence orbitals, the s and
two of the p's, are hybridized to give three sp2 hybrid
orbitals, leaving one pure
atomic p orbital unchanged. |
 |
| Summary of the effect of various perturbing
geometries on the s/p valence shells in a central atom.
By "vacuum" is meant the atom in isolation from
any external influence. |
 |
| For expanded octets, the d orbitals come into
consideration. There are five d orbitals (since d implies
the angular momentum quantum number l = 2 and hence ml
= -2, -1, 0, +1, +2. The trigonal bipyramid and
octahedral geometries involve five and
six hybrids as indicated. |
 |
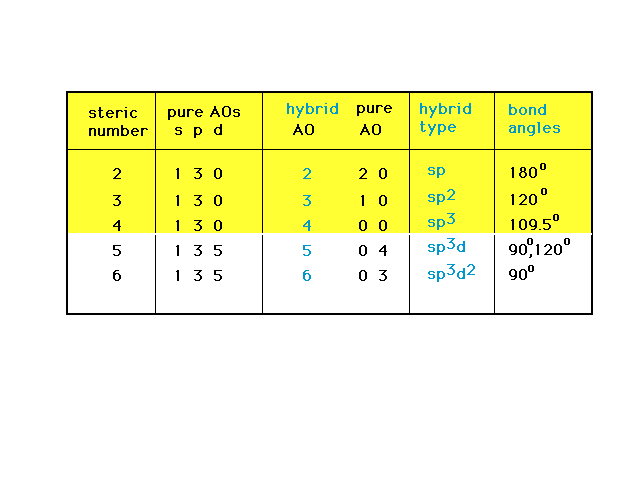
| An overview of the relationship among steric
number, and the number and types of pure and hybrid
orbitals associated with the implied geometries. |
 |
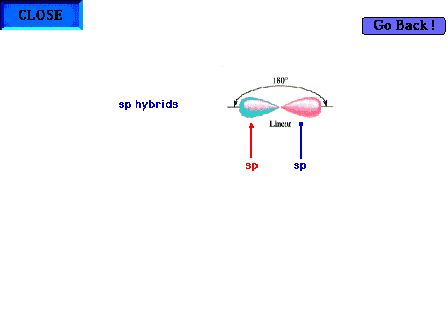
| An illustration of a central atom's two sp hybrid
orbitals present for a linear geometry about the central
atom. Bear in mind that it is implied that there are also
two pure pure p orbitals (not shown) perpendicular to the
indicated axis. |
 |
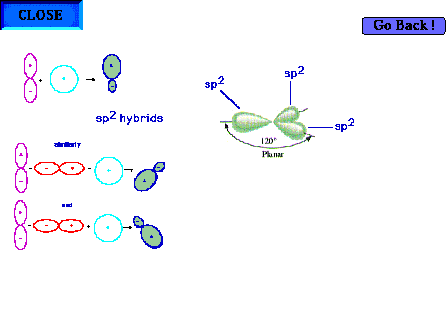
| Three sp2 hybrid atomic orbitals,
constructed in some detail on an earlier slide, showing
their trigonal planar directionality. It is implied that
there is one remaining pure p atomic orbital
perpendicular to the plane shown. |
 |
| Moving on to construct the chemical bonding situation
in polyatomic molecules, we will assemble an ethylene
structure piece by piece. |
 |
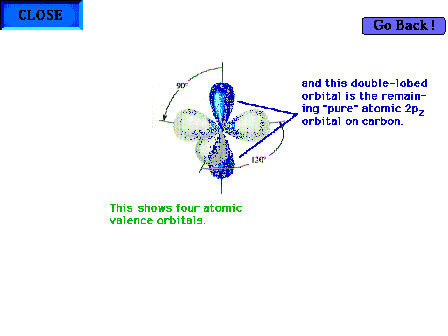
| The atomic orbitals for carbon in ethylene
highlighting the one pure 2p atomic orbital
perpendicular to the plane of the three hybrid sp2
orbitals. |
 |
| Assembling the ethylene molecule showing the overlap
between the various pairs of atomic orbitals (which can
be pure or hybrid). |
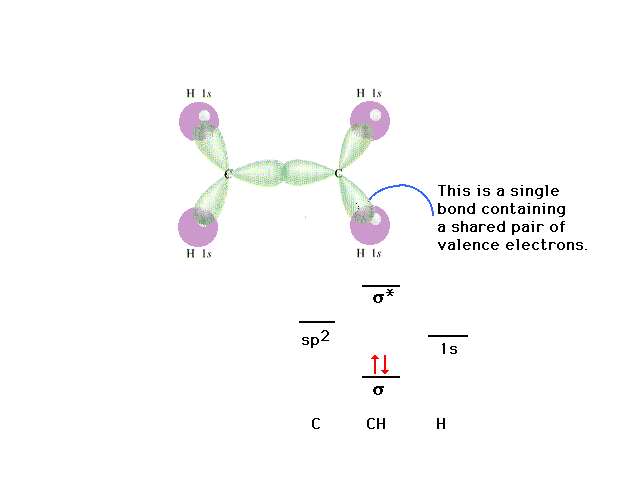 |
| The C-H "sigma" bond. The "sigma"
label comes from the symmetry (appearance) of the
electron distribution about the bond axis. When viewed
directly down the bond axis, the profile resembles the
atomic s-orbital profile. Hence the "sigma"
term. |
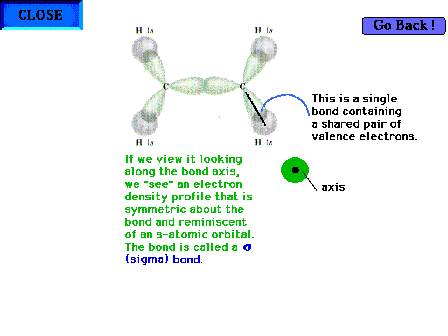 |
| The C-C "sigma" bond. The profile of the
implied electron distribution about the bond axis is
similar to that on the previous slide for the C-H sigma
bond. |
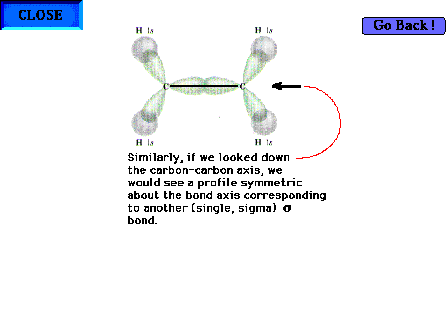 |
| Rotating the molecule 90o about the C-C
bond axis so that the structure's plane is perpendicular
to the point of view brings the pure 2p atomic orbitals
into view (since they are perpendicular to the sp2
hybrid orbitals). |
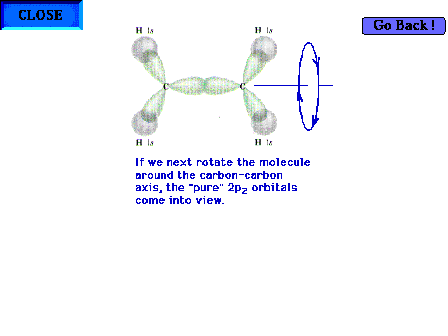 |
| Looking down the C-C axis again to determine the
geometric appearance of the electron density in this new
region of overlap. |
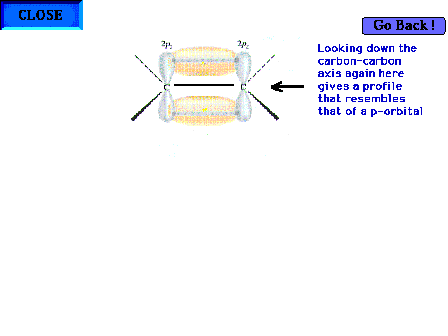 |
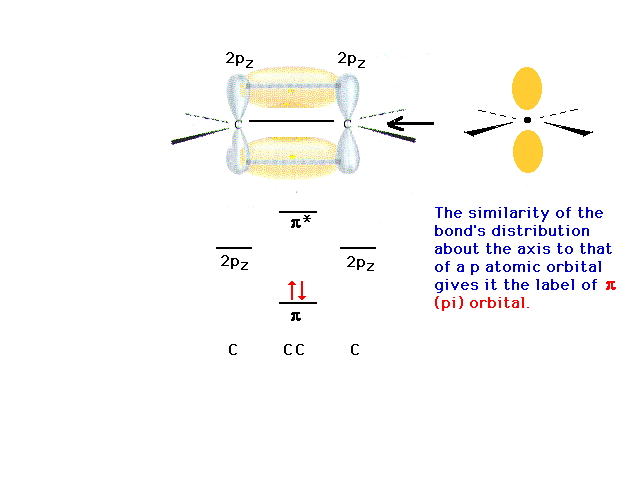
| The final description of bonding in ethylene would
be: Each CH bond is a sigma from (1sH + sp2C).
The CC bond is a sigma from (sp2C +
sp2C) and a pi from (2pC
+ 2pC). |
 |
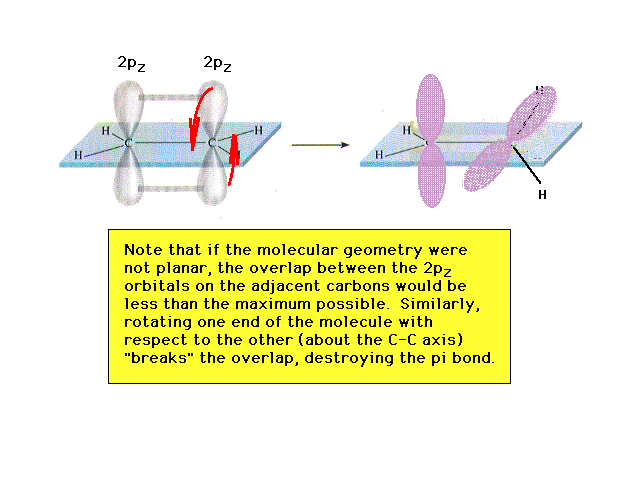
| Rotation about the C-C bond axis, giving an ethylene
molecule which is not entirely planar, shows that
non-planarity involves disrupting the overlap between the
two 2p orbitals, breaking the pi-bond. Breaking a bond
takes energy. Consequently, the most stable geometry of
the molecule is planar and disturbing the planarity can
be accomplished only at the cost (input) of energy. |
 |
| Returning to orbitals in polyatomic molecules,
we look at the construction of molecular orbitals for
each bond in HCCH. |
 |
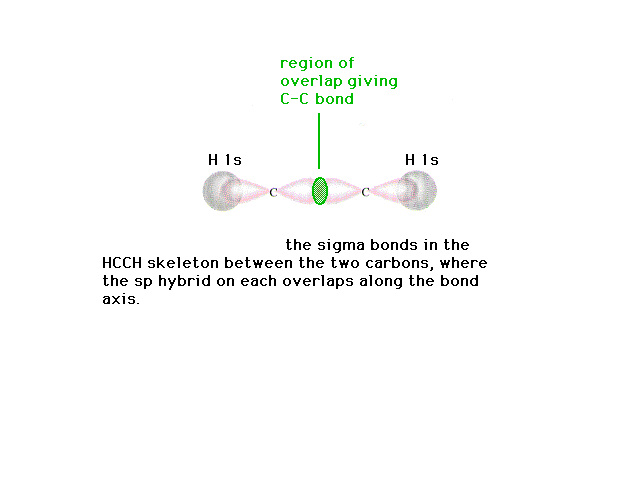
| The CC sigma bond is "constructed" from
linear combinations of the carbon atomic orbitals (now
hybrid atomic orbitals in a polyatomic system). |
 |
| Perpendicular to the sp hybrids on each carbon are
the pure 2p atomic orbitals which can lead to pi-bond
formation. |
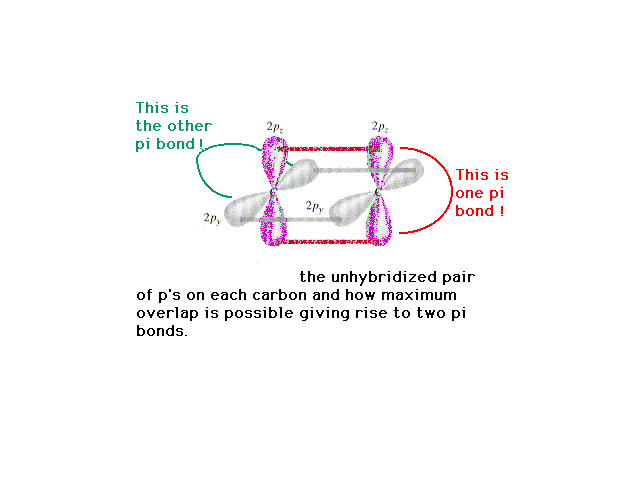 |
| Here we show the full set of orbital shapes
occupied by valence electrons in HCCH. |
 |
| Consider formaldehyde next. The Lewis structure
allows us to infer atomic orbitals for valence electrons
as indicated. |
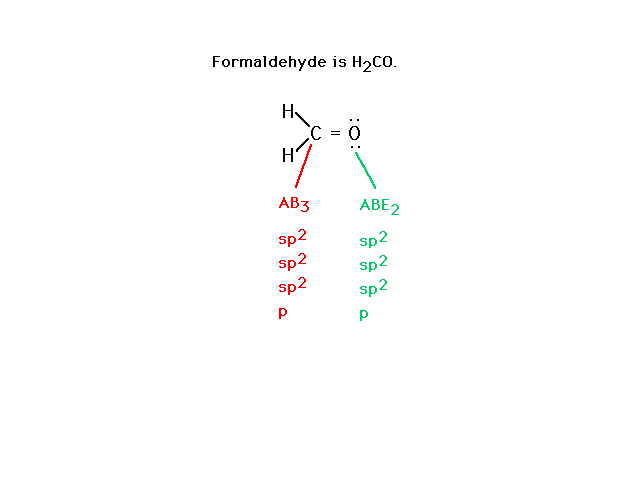 |
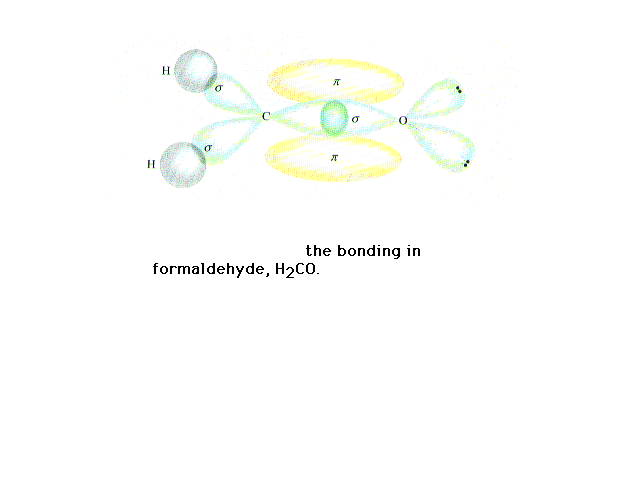
| The orbitals in formaldehyde occupied by valence
electrons. |
 |