| Lecture
#25 |
| |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture Outline |
Molecular Orbitals (delocalized)
Energies via particle-in-a-box
Conjugated systems
Strained bonds
Metallic bond
|
| Here we have a more delocalized system in which the
absorbed wavelength has consequently shifted to the
visible region of the electromagnetic spectrum and the
highest occupied orbital starts out with a larger n
quantum number. |
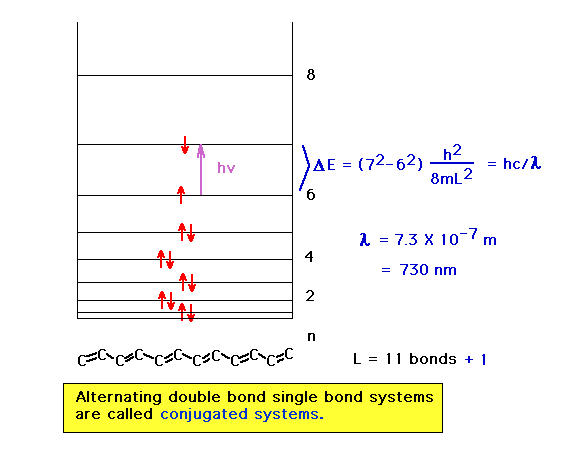 |
| We began the look at delocalized molecular orbitals
with a discussion of the (energy and geometry) properties
of 1,3 butadiene, indicating that we could understand
them if the central CC bond had some double bond
character. |
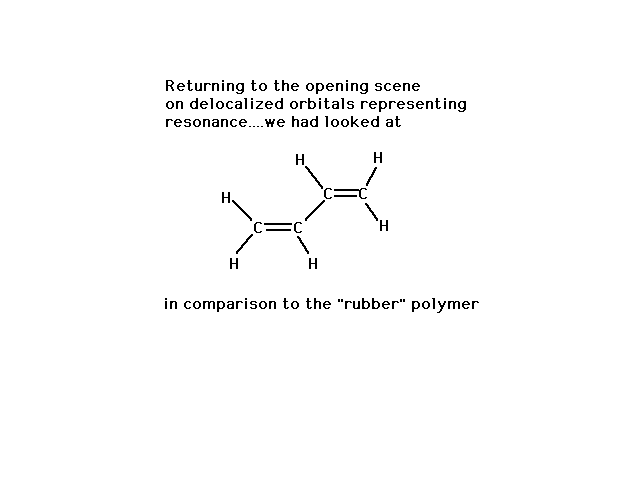 |
| Yet just previously, we noted a similar looking
structure had the flexibility associated with
unrestricted rotation about a sigma bond. |
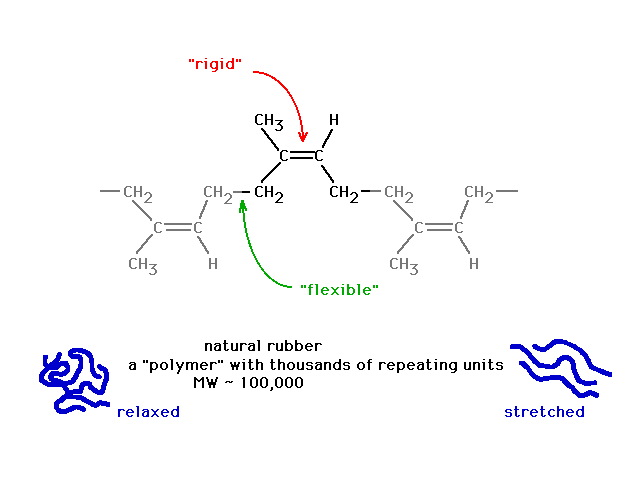 |
| The difference, reminding us of what leads to
delocalized molecular orbitals, is revealed in looking in
more detail at the situation where we do get unrestricted
rotation, starting here... |
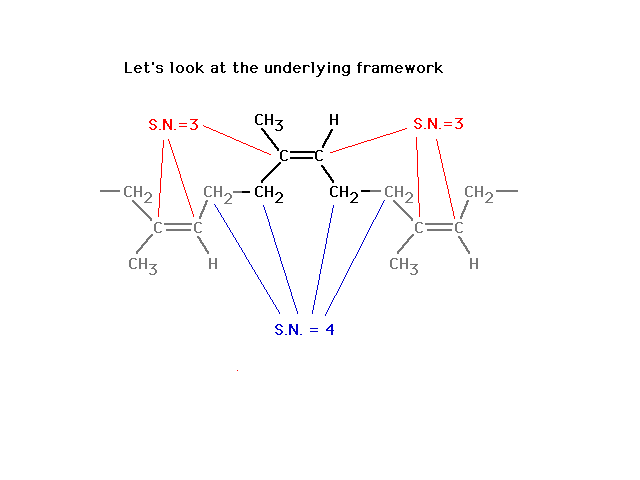 |
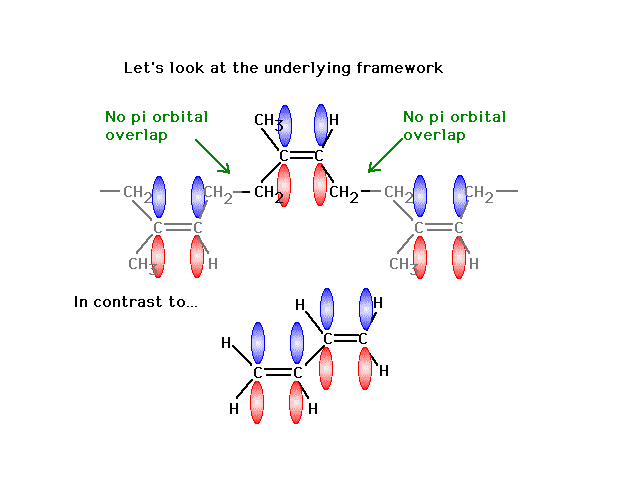
| Finally, a look at the atomic orbitals shows that in
"rubber" one gets localized pi bonds whereas in
the butadiene, delocalized pi bonds arise. |
 |
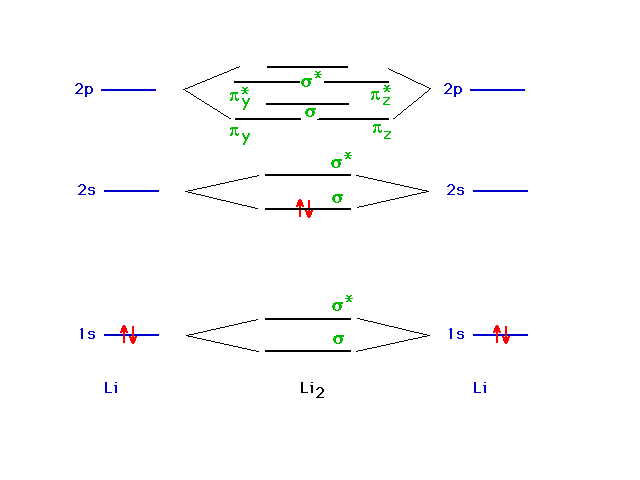
| Another major application of the particle-in-a-box
model is to describe bonding in metals. We will begin our
discussion with a chain of lithium atoms starting with Li2. |
 |
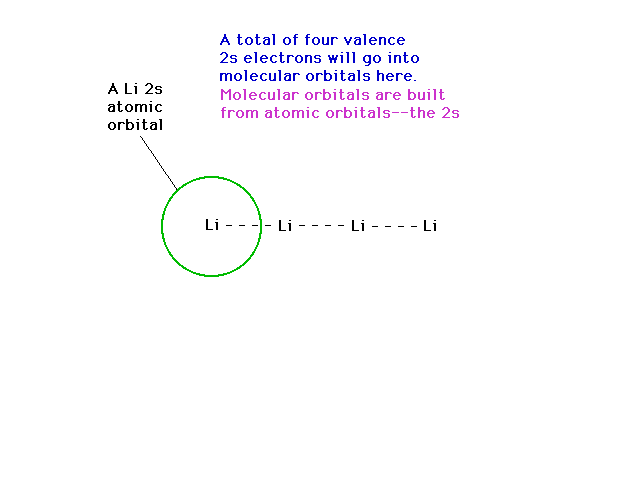
| If we next go to Li4, we can note, soon
enough, that delocalized molecular orbitals are possible
using 2s atomic orbitals. |
 |
| Overlap! |
 |
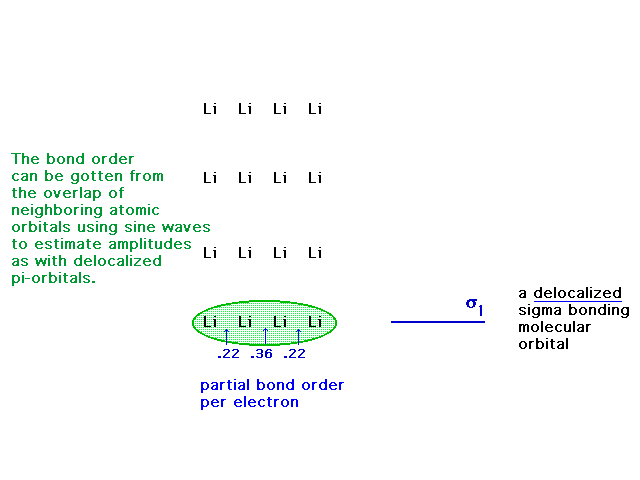
| The four atomic 2s orbitals can overlap
constructively to give the indicated molecular orbital
which is delocalized over the four nuclei (and their
inner 1s cores). |
 |
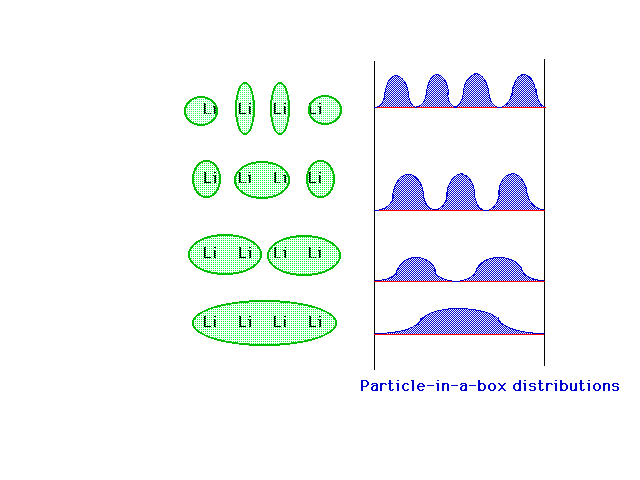
| Shown on the left are the four delocalized
combinations, which look somewhat like the delocalized pi
orbitals we derived for 1,3 butadiene -- H2C=CH-CH=CH2. One
the right are the four lowest particle-in-a-box density
distributions which do a fairly good job of representing
the delocalized molecular orbitals on the left.
|
 |
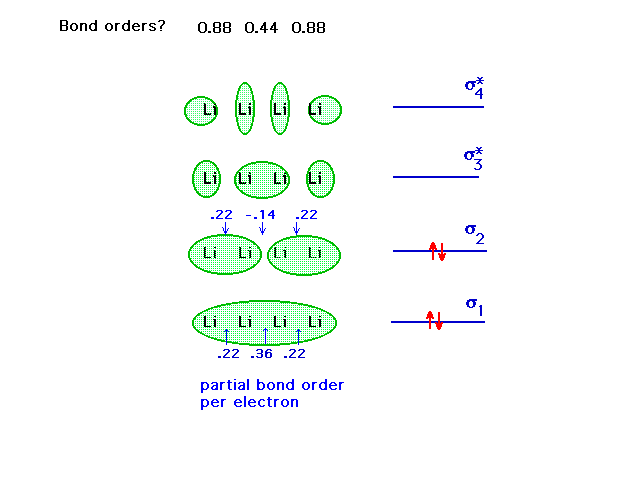
| The diagram contains the 'bond order per electron'.
Multiple each such partial bond order by the number of
electrons delocalized over the level and add up the
contribution from each level...at each bond. Example:
2*(,22)+2*(.22)=.88 |
 |
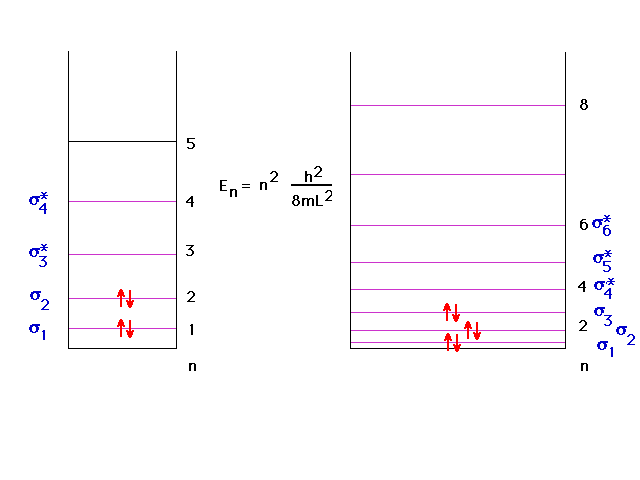
| Since the particle-in-a-box does
"okay", we can use it to get some information
about energy levels associated with delocalized orbitals,
information that was missing so far. |
 |
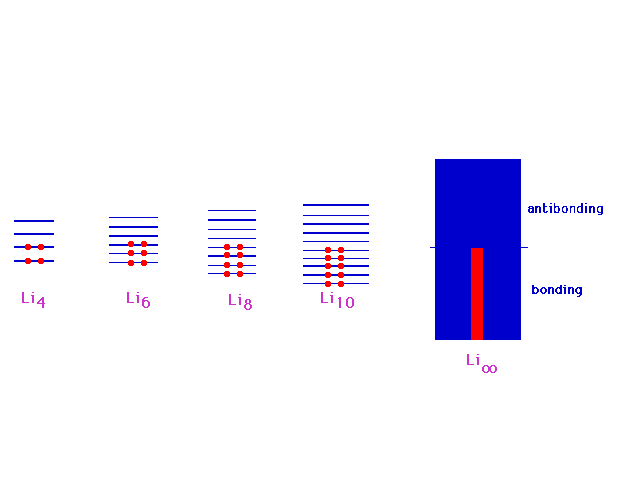
| In continuing to build longer and longer chains
of lithium molecules, the levels fill in a simple way,
indicated here, with a big jump going to macroscopic
amounts (Avogadro's number) of lithiums in one long
molecule. This will be the basis of our understanding of
the metallic bond. |
 |
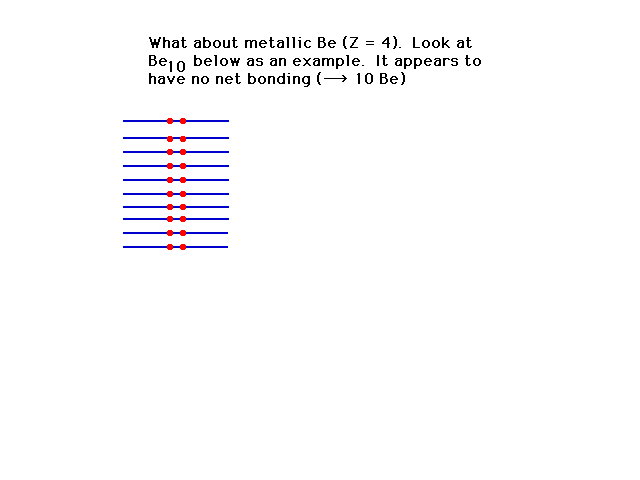
| Next to lithium on the Periodic Table is
beryllium, but the levels seem to fill to the top.
(Bonding and antibonding are equally occupied and there
seems to be no metallic bond possible. |
 |
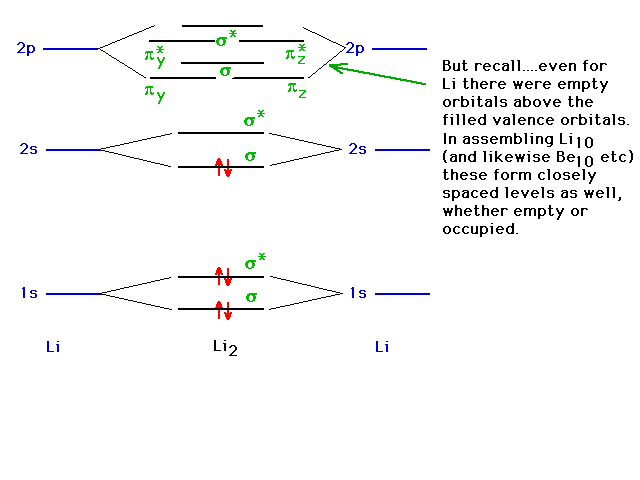
| However, remember that there are more levels that
could come into play. |
 |
| Above the 2s lie the 2p orbitals which contribute
another band of levels. The last electrons occupy pi
bonding orbitals in the 2p band. There are enough bonding
delocalized molecular orbitals for all the valence
electrons to be considered delocalized and the system
bound as one giant molecule. |
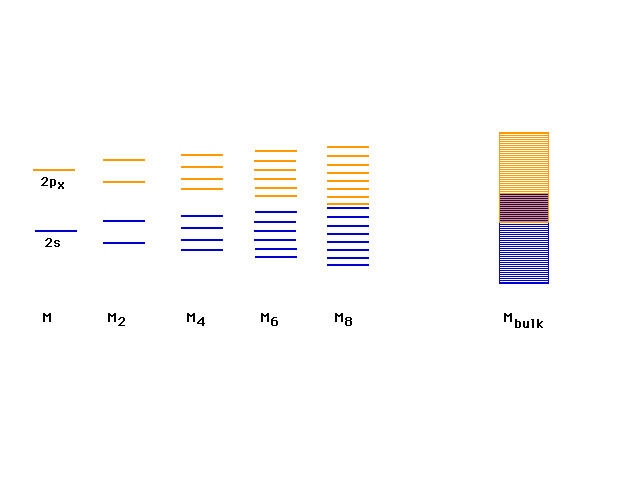 |
| If we consider boron and carbon instead of beryllium,
the 2s-2p splitting grows. |
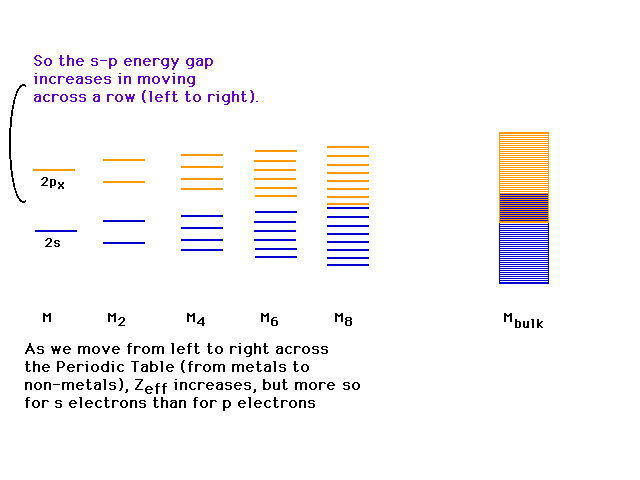 |
| Eventually, as we approach the right side of the
periodic table, the 2s-2p are far enough apart that the
two bands originating there no longer overlap. There is
now an energy gap that most be overcome to access
delocalized orbitals spread over the giant molecule. If
the energy needed to move an electron into one of these
available conducting orbitals is large, we have an
electronic insulator, since the electrons are essentially
confined to the lower band. |
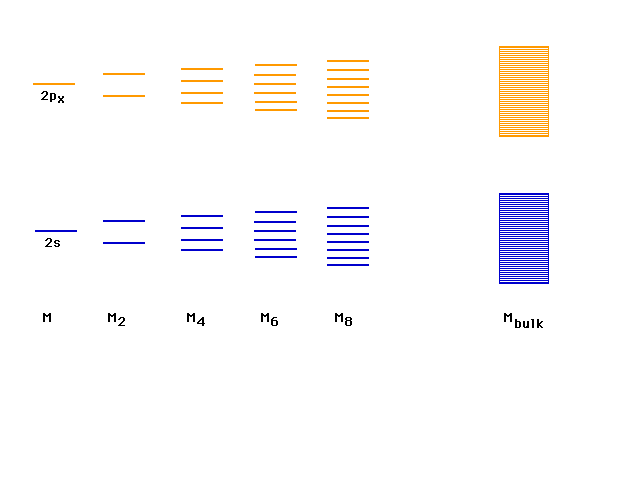 |



