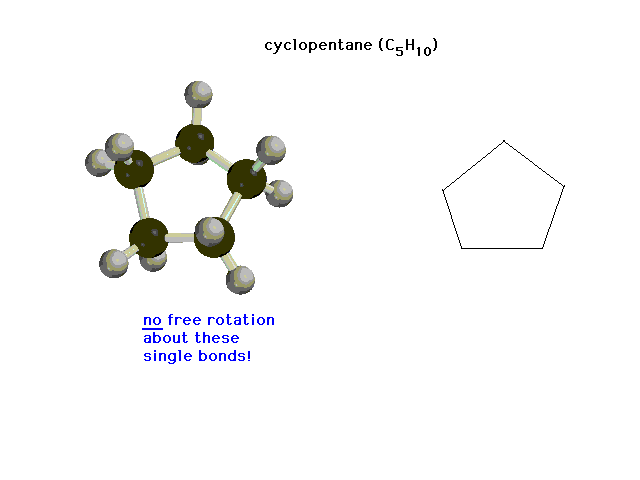| Lecture
#23 |
| |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture Outline |
Molecular Orbitals in Polyatomic
Molecules (Localized Bonds)
Rings
Strained bonds
Molecular Orbitals in Polyatomic Molecules
(Delocalized Bonds)
Bond orders
Partial bond order per electron
1.3 butadiene
|
| Here we have sigma bonds, but free rotation is
blocked by their incorporation into a ring structure. |
 |
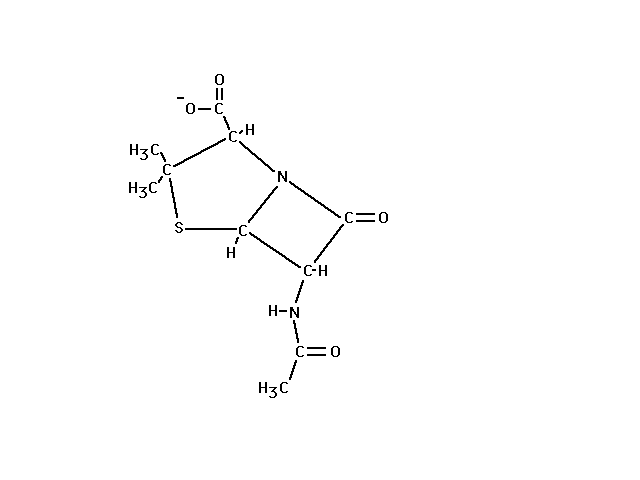
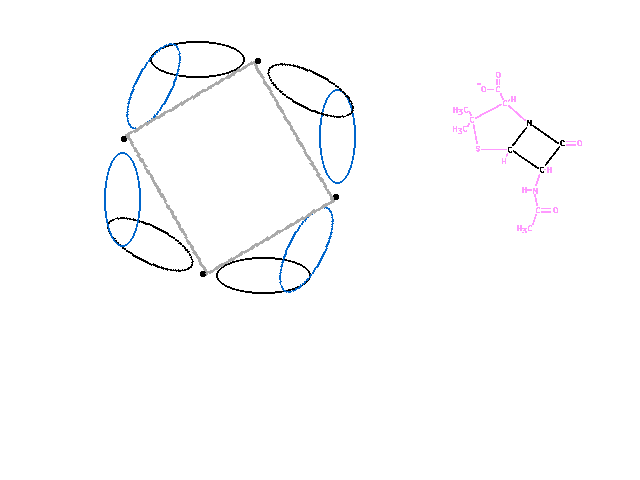
| This is penicillin, one of many variations of the
well-known antibiotic. |
 |
| The five-membered, if a perfect pentagon, would
have 108 degree bond angles. The corner atoms of the ring
have tetrahedral geometry with 109.5 degree angles
between hybrid atomic orbitals allowing effective overlap
with neighborinring atomic orbitals. |
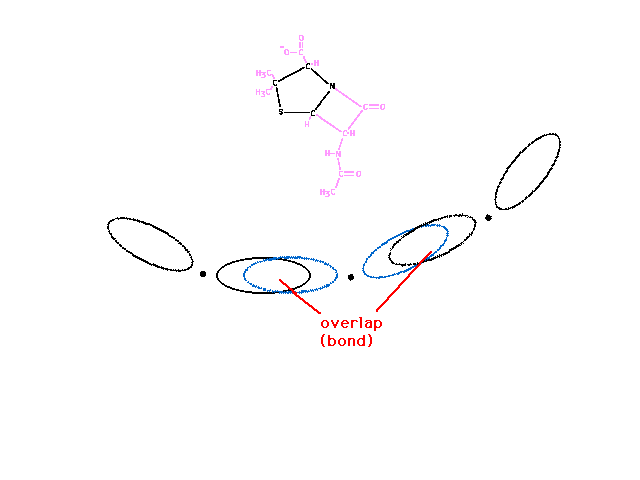 |
| In the four-membered ring, the bond angles are
~90 degrees, causing the overlap between neighboring
orbitals to be much less effective (less region of
constructive interference) since they spread to larger
angles. |
 |
| The topic of molecular orbitals is extended to
systems in which the orbitals encompass more than just
two centers -- atoms -- and are referred to then as
delocalized orbitals, in contrast to our previous
discussion of localized orbitals (between just two
atoms). |
 |
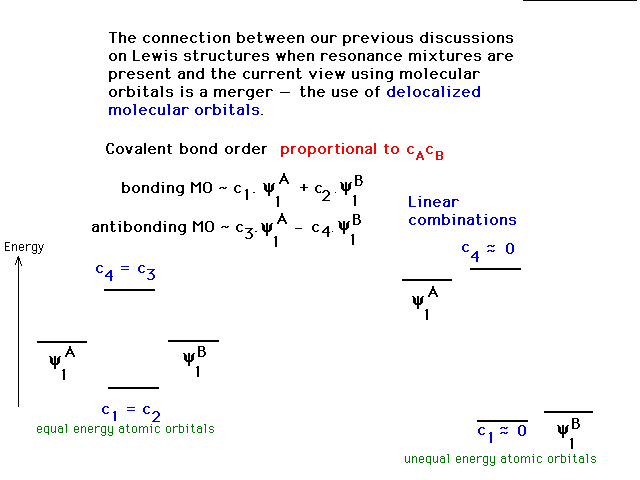
| A non-essential view of the role that the
"coefficients" play in determining bond
properties. The coefficients, c, actually emerge when the
linear combinations are plugged into the Schrodinger
Equation. The bond order that results for a link between
A and B is then proportional to the product cAcB
and can be positive (bonding), negative (antibonding), or
zero (non-bonding). This may be useful
to your comfort level, but is not critical. |
 |
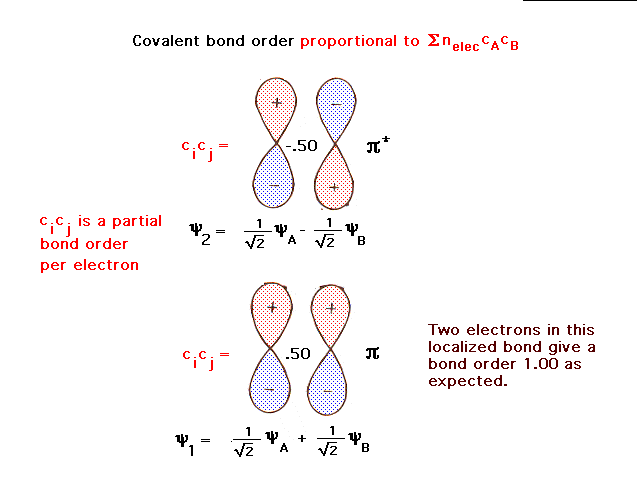
| For two identical atoms coming together, the atomic p
orbitals perpendicular to the bond axis form constructive
and destructive combinations shown more rigorously here. |
 |
| Using a four-carbon system whose Lewis structure
indicates has two double bonds and one single bond, we
will show the molecular orbitals describing the pi
bonding are delocalized. |
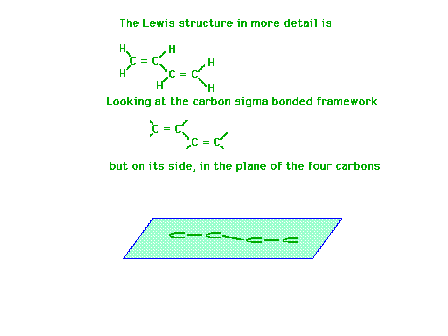 |
| Each carbon atom has a sigma framework involving sp2
orbitals leaving a pure 2p atomic orbital from which the
pi molecular orbital will arise. |
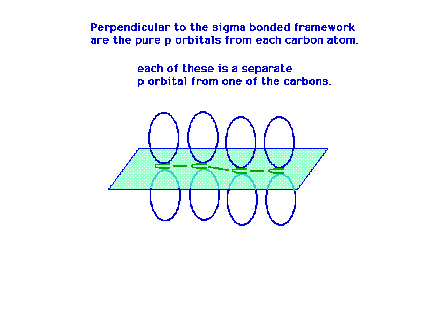 |
| One of the linear combinations of the four atomic 2p
orbitals is entirely constructive -- in phase over all
four atoms -- and its resulting delocalized bonding
molecular orbital allows any electrons it contains to be
"spread" over the entire structure. The
computer-generated "true" result is shown as
well. |
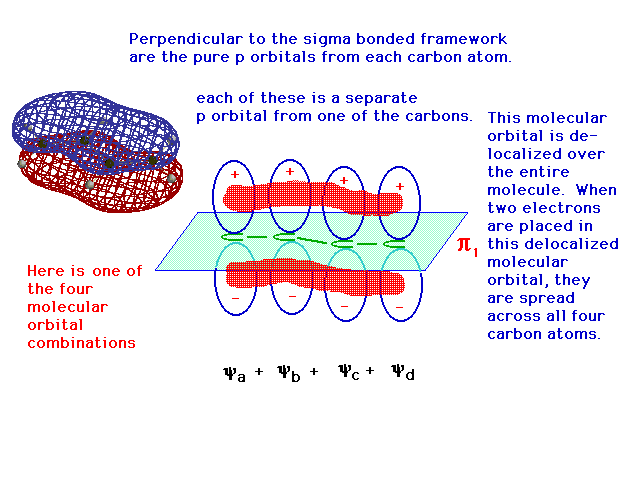 |
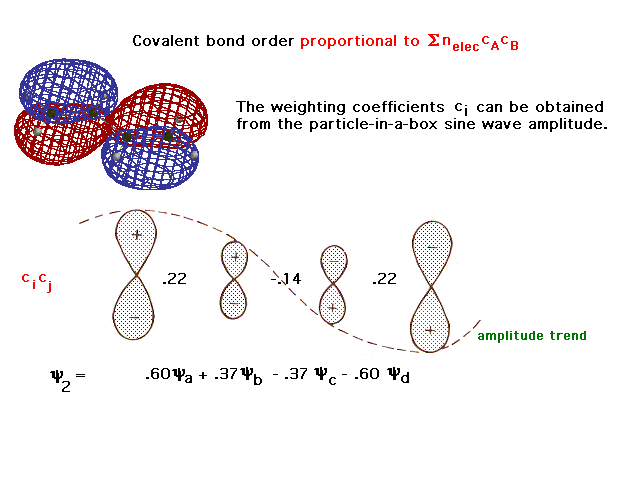
| The rigorously calculated molecular orbital wave
function has coefficients shown here, from which the
partial bond order per electron, cicj
between linked atoms, may be calculated. Starting from
the left carbon, c1*c2 = .37 * .60
= .22. Each electron in this first orbital contributes a
pi bond order of .22 to the structure. |
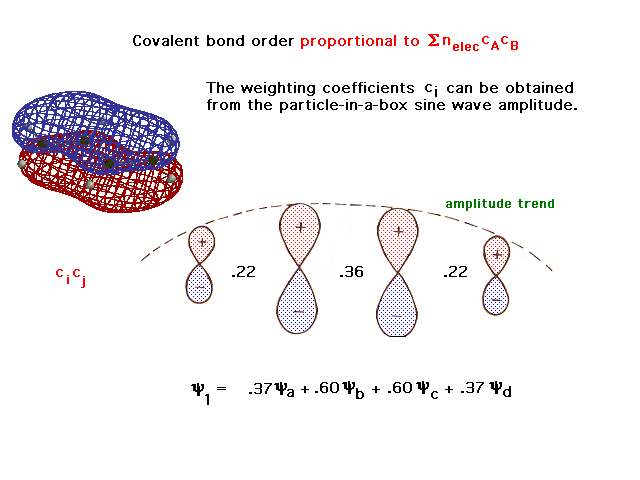 |
| Another of the four combinations of the four atomic
orbitals is shown here. This is also a bonding molecular
orbital. |
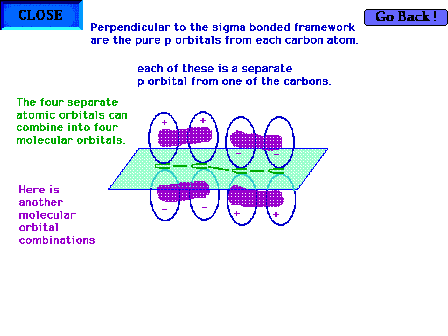 |
| More rigorous picture and computer generated view of
the second delocalized molecular orbital in the
butadiene. |
 |
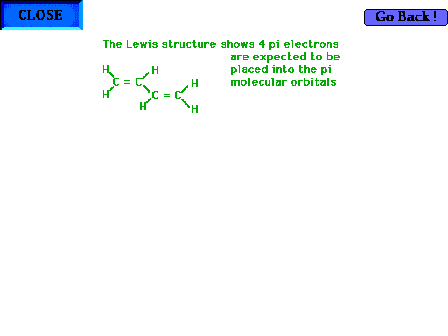
| A look at the original Lewis structure reminds us
that there are four pi electrons -- two from each of the
"double" part of the double bonds -- to be
distributed into the pi molecular orbitals. |
 |
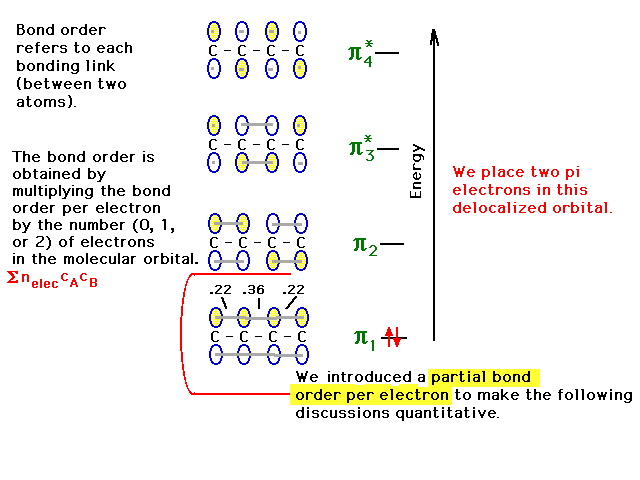
| Placing one of the pairs of pi electrons into the
lowest orbitals allows us to calculate the bond order due
to these electrons at each carbon-carbon link. We
introduce the idea of a partial bond order per
electron associated with each interatomic link for
each molecular orbital. Here, that partial bond order per
electron is half the result we got for the pair of
electrons or one-sixth for each CC link in pi orbital
#1.The bond order -- one-half the average number of
electrons per bond -- may be obtained from a given bond's
partial bond order per electron by multiplying
by the number of electrons in the orbital. Vice
versa, if you knew how the
electron(s) in a given molecular orbital were distributed
over the various links, you could get the partial
bond order per electron as we did for the lowest
pi-orbital. |
 |
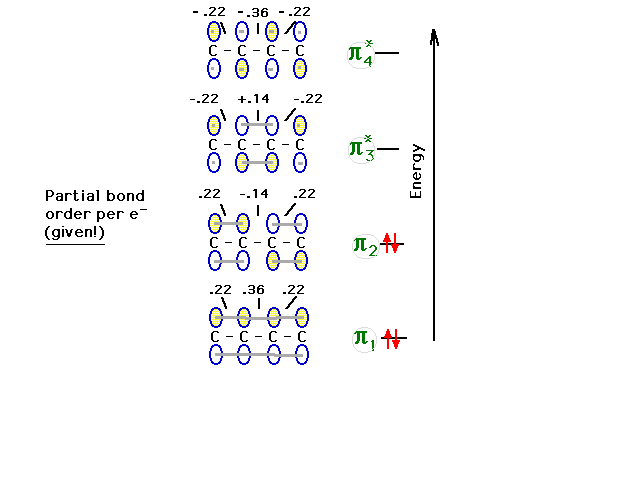
| The remaining (second) pair of pi electrons goes into
the next state. We again calculate the bond order at each
carbon-carbon link due to these two electrons from the partial
bond order per electron that would be given. .
|
 |
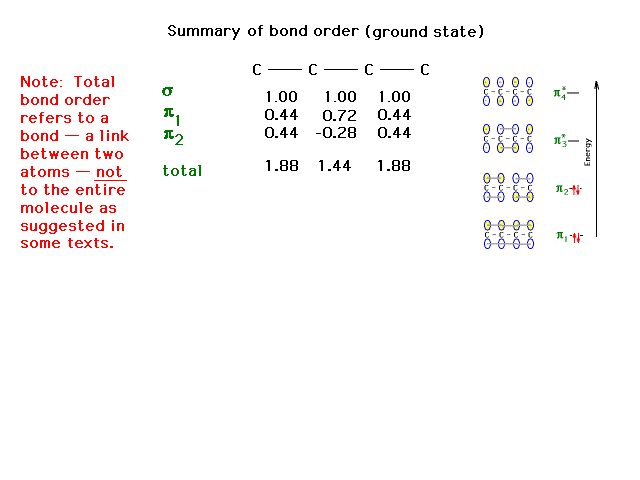
| The complete bond order for each carbon-carbon link
with contributions considered from the sigma and pi
molecular orbitals summed. |
 |
| The difference in the molecule's structure when
molecular orbital theory is used can be accommodated with
resonance Lewis structures that are not what we call
"preferred" structures, but which nevertheless
affect the overall appearance of the molecule. The bonds
are neither pure double bonds nor pure single bonds. |
 |
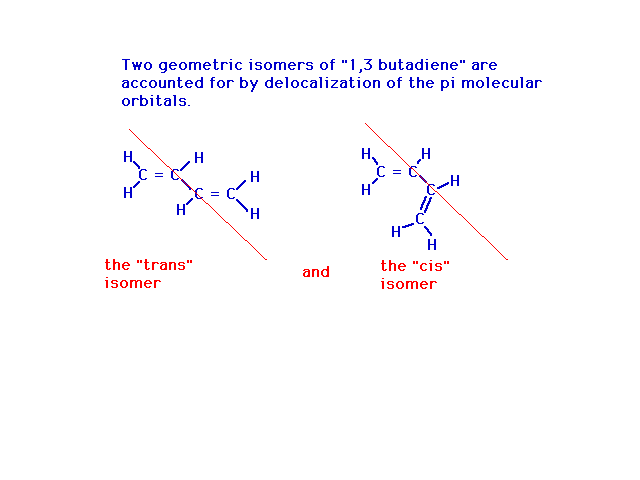
| Another property of the molecule that is revealed
here is that, because the central bond is not a freely
rotating single bond, but rather has partial double bond
character restricting rotational motion, there can be two
geometrical (cis-trans) isomers. |
 |