| Lecture
#19 |
| Text: Starting Chapter 14 at Section 2 |
| CURMUDGEON
GENERAL'S WARNING. These "slides"
represent highlights from lecture and are neither
complete nor meant to replace lecture. It is
advised not to use
these as a reliable means to replace missed
lecture material. Do so at risk to healthy
academic performance in 09-105. |
|
| Lecture Outline |
Quantum Theory of the Chemical Bond
Molecular orbitals (in "homonuclear diatomic
molecules"
Approximated by combinations of atomic
orbitals
Constructive and
destructive interference effects
Combining 1s atomic
orbitals to get molecular orbitals
"Sigma" bonding molecular
orbital
"Sigma" antibonding molecular
orbital
Combining 2p atomic orbitals
"Sigma" bonding molecular
orbital
|
| Recall all that you've learned about wave functions
and atomic orbitals, because we now start the adventure
with electron behavior in molecular systems and develop
the modern theory of the chemical bond. |
 |
| Solving the Schrodinger wave equation for a system in
which there is more than one center of force (a single
nucleus) is difficult. Just a few years ago, John Pople,
retired Professor of Chemistry at Carnegie Mellon, shared
the 1998 Nobel Prize in Chemistry
for devising mathematical tools amenable to computation
that have greatly eased the problem if one resorts to
using a computer. Approximate wave functions can be
assembled using the ones we're already intimately
familiar with: the hydrogen-like, one-electron atomic
orbitals. |
 |
| Among the unusual properties associated with the
mathematics of waves is that of "interference".
This occurs even for classical waves such as water waves
and sound waves. Depending on whether combining waves
have the same sign of their amplitudes or opposite signs,
(i.e. they are in phase or out of phase,) the
waves interfere constructively or destructively,
respectively. As usual, we will visualize the complicated
multidimensional appearance of the wave amplitudes by
contour outlines in 2-D. |
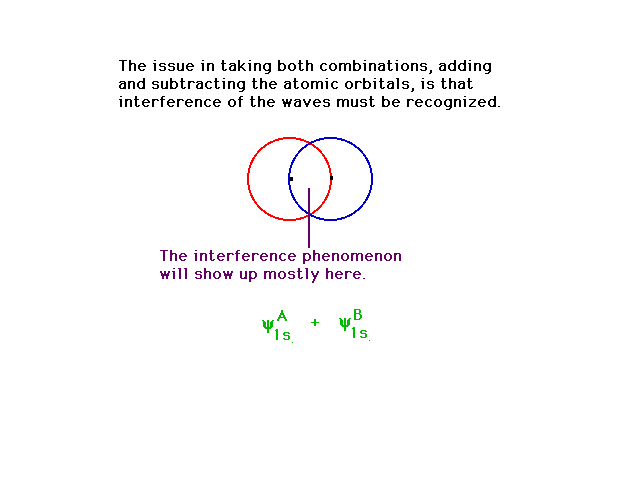 |
| If we add together a 1s atomic orbital on one
hydrogen atom with an identical 1s atomic orbital
centered on another nucleus, the resulting orbital
(whether there are electrons there or not) closely
resembles the more exact orbital one would calculate by
highly sophisticated mathematical techniques.Recalling
the significance of an orbital, this would then indicate
where an electron would be expected to be found if we
placed an electron in the system. It would also be used
to calculate the energy such an electron would have.
Energy and geometry are our recurring themes, n'est
pas? |
 |
| This is a calculated solution for the constructive
interference result. |
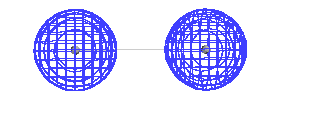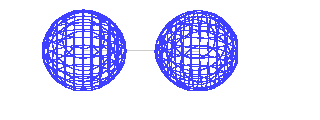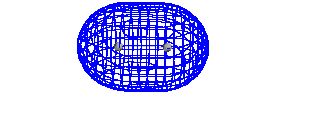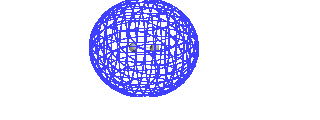 |
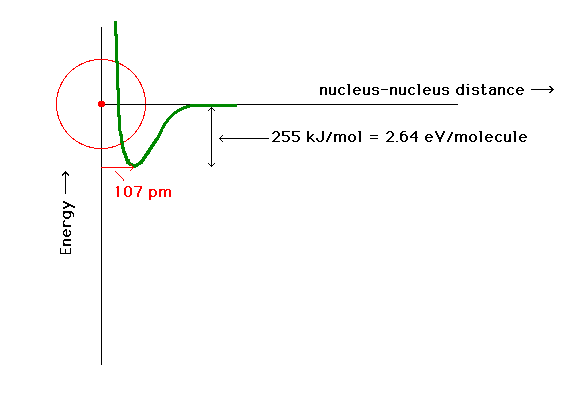
| An electron in an orbital about two protons has a
potential energy indicated by the heavy curve if
constructive interference of the atomic orbitals
represents the electron's orbital. There is a certain
proton-proton distance at which the energy is minimum.
This is close to the bond length in the system with one
electron. |
 |
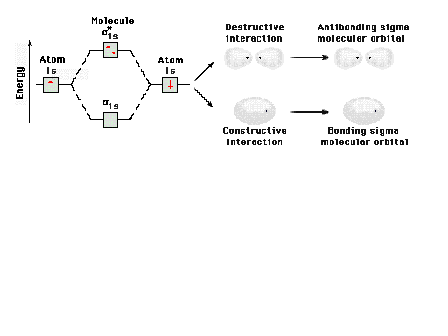
| If destructive interference represents the orbital in
which the electron happens to be found, the linear
combination results in a depeletion of electron density
between the positively charged protons. They repel each
other under these circumstances. |
 |
| If destructive interference represents the orbital in
which the electron happens to be found, the linear
combination results in a depeletion of electron density
between the positively charged protons. They repel each
other under these circumstances. |
 |
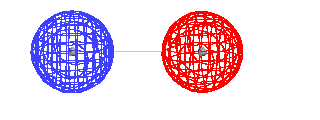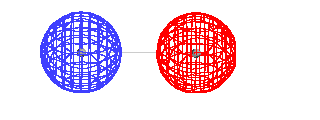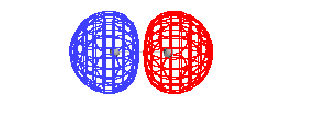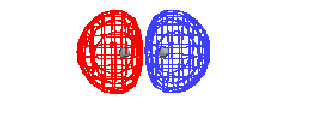
| This is the destructive interference combination of
1s atomic orbitals |
 |
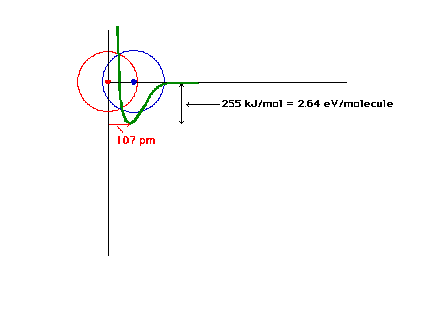
| The total energy of the ground state of H2+
as a function of the distance between the protons. |
 |
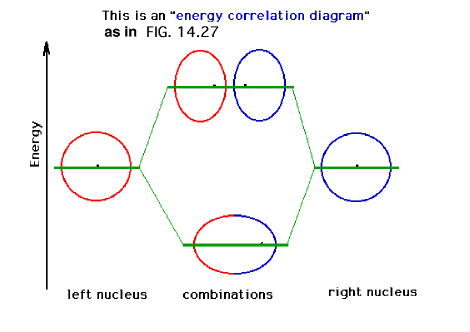
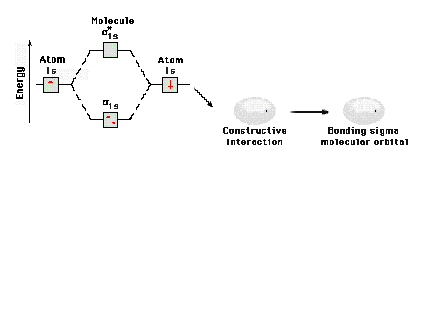
| A schematic of the orbitals on separated protons
relative to "close" protons. The constructive
combination of atomic orbitals gives rise to a system
lower in energy than the isolated system and is a bonding
molecular orbital. |
 |
Energy diagram and geometry for the 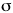 -1s (bonding) orbital construction. -1s (bonding) orbital construction.
|
 |
Energy diagram and geometry for the 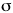 *-1s (antibonding) orbital
construction *-1s (antibonding) orbital
construction
|
 |
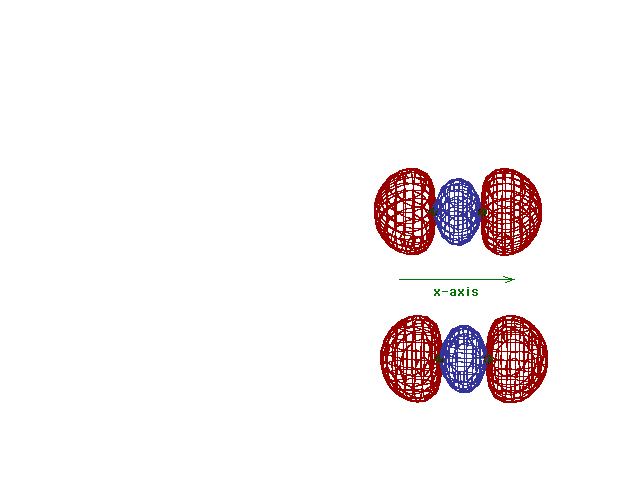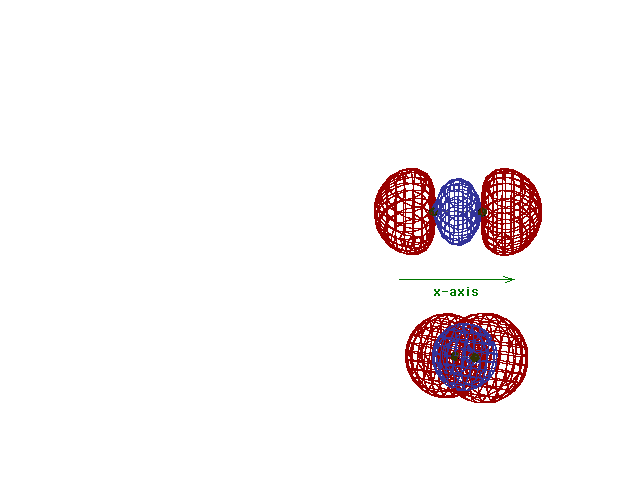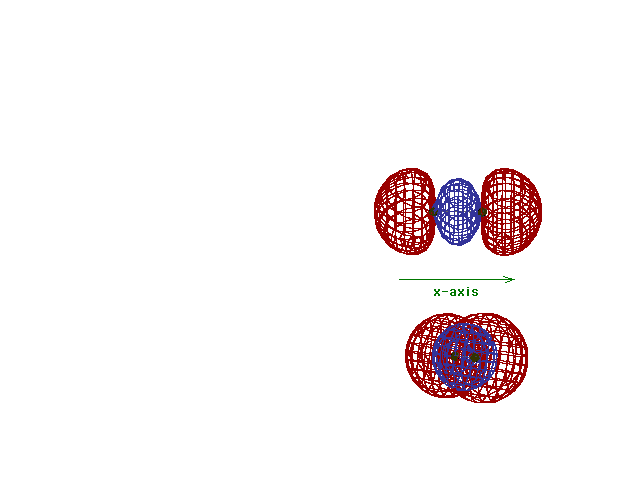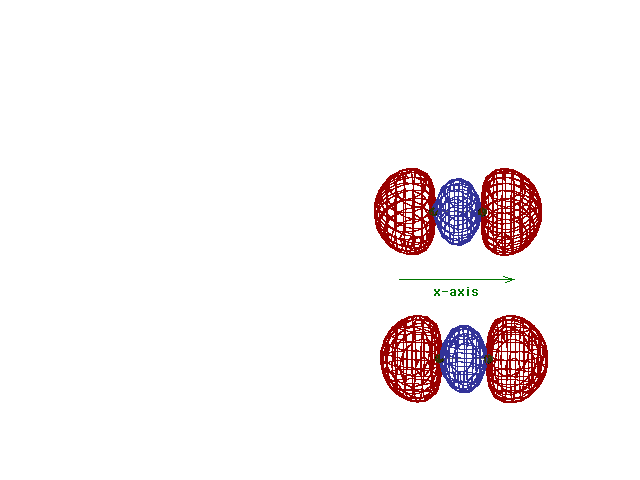
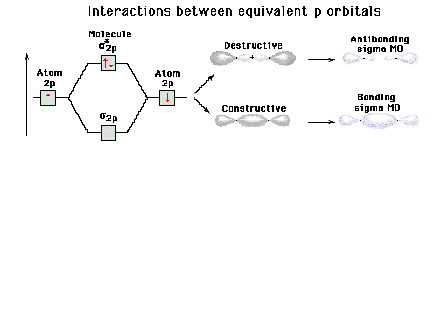
| Energy diagram and geometry for the sigma-2px
(bonding) orbital construction from the 2p atomic
orbitals originally directed along the bonding (x) axis. |
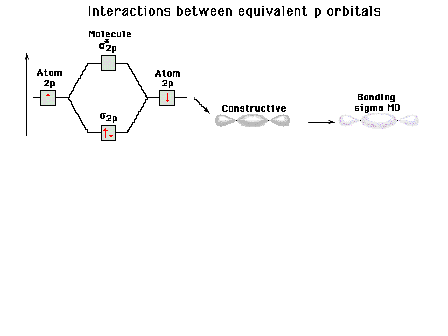 |
This (with luck) is an animation of the
computer-generated 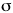 2p
(or 2p
(or 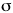 p) bonding
molecular orbital showing how the symmetry about the bond
axis resembles that for the s-atomic orbital's symmetry
about the nucleus. Hence the p) bonding
molecular orbital showing how the symmetry about the bond
axis resembles that for the s-atomic orbital's symmetry
about the nucleus. Hence the 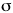 label. label. |
 |
Energy diagram and geometry for the 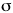 *-2p (antibonding) molecular orbital
construction *-2p (antibonding) molecular orbital
construction |
 |
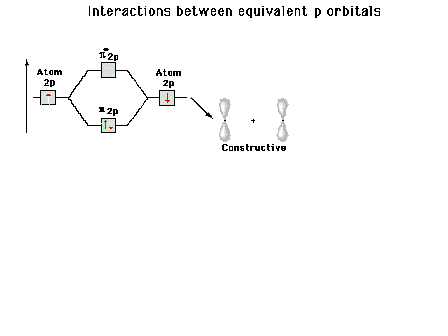
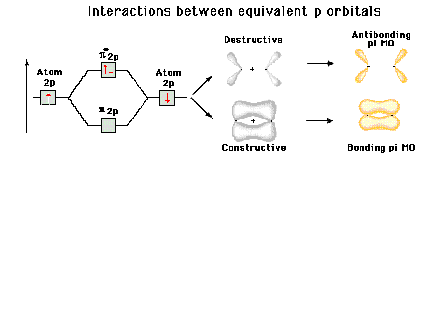
| A reminder that, perpendicular to the bond axis in
the x-direction, there are 2p atomic orbitals in the
z-direction and in the y-direction. Just the 2py
orbitals on each atom are shown here. |
 |
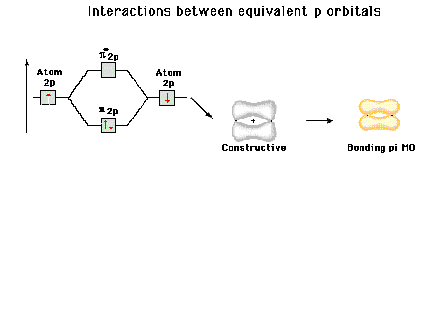
Energy diagram and geometry for the 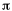 -2py
(bonding) molecular orbital construction from the 2p
atomic orbitals originally pointing in the y-direction,
perpendicular to the bond axis and in the plane of the
illustration. Constructive interference occurs in the
region of overlap. (Recognize that there is an identical
pi bonding level, same energy, constructed in the
x-direction from the 2pz atomic orbitals.) -2py
(bonding) molecular orbital construction from the 2p
atomic orbitals originally pointing in the y-direction,
perpendicular to the bond axis and in the plane of the
illustration. Constructive interference occurs in the
region of overlap. (Recognize that there is an identical
pi bonding level, same energy, constructed in the
x-direction from the 2pz atomic orbitals.) |
 |
This is an animation of the computer-generated 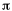 2p
bonding molecular orbital showing how the symmetry about
the bond axis resembles that for the p-atomic orbital's
symmetry about the nucleus. Hence the 2p
bonding molecular orbital showing how the symmetry about
the bond axis resembles that for the p-atomic orbital's
symmetry about the nucleus. Hence the 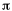 label. label. |
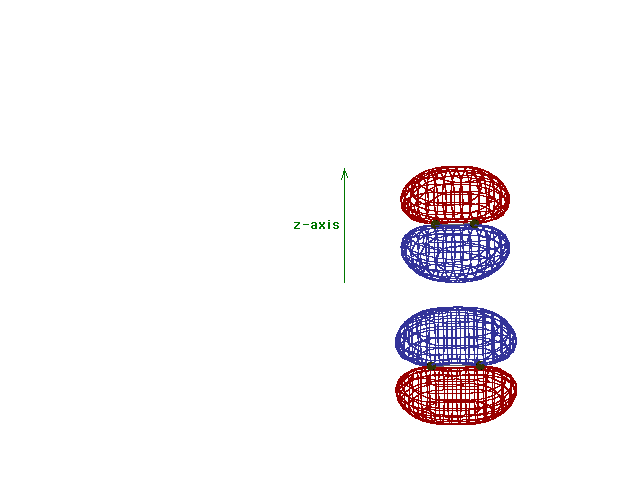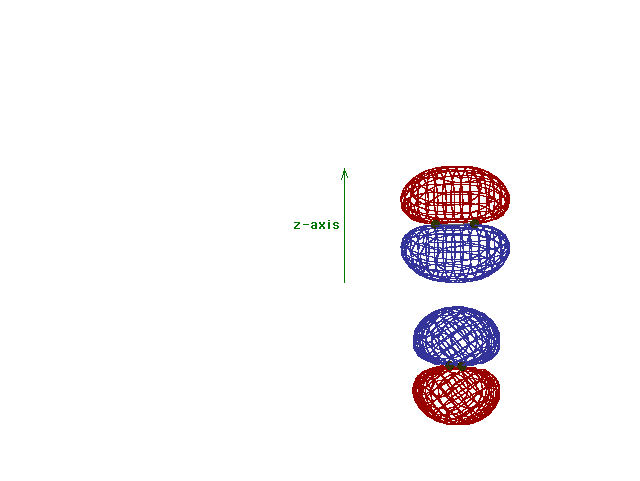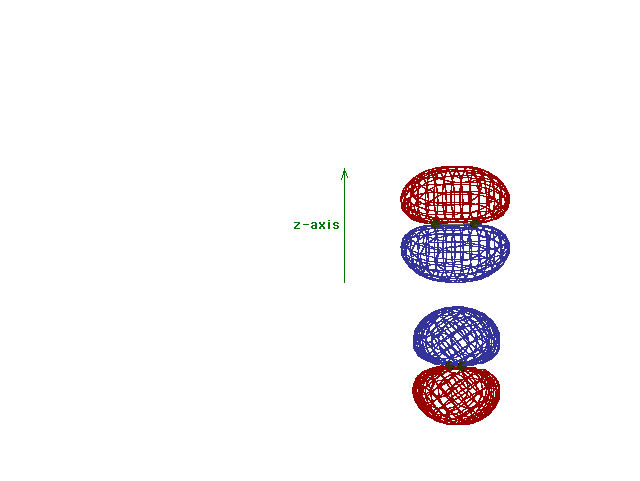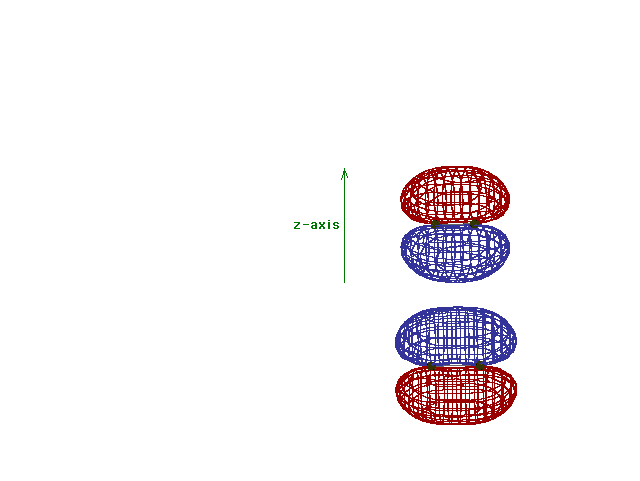 |
Energy diagram and geometry for the  *-2py
(antibonding) molecular orbital construction from the 2p
atomic orbitals originally pointing in the y-direction,
perpendicular to the bond axis and in the plane of the
illustration. Destructive interference occurs here, in
contrast to what occurs for the bonding molecular
orbital. (Recognize that there is an identical *-2py
(antibonding) molecular orbital construction from the 2p
atomic orbitals originally pointing in the y-direction,
perpendicular to the bond axis and in the plane of the
illustration. Destructive interference occurs here, in
contrast to what occurs for the bonding molecular
orbital. (Recognize that there is an identical 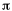 *
antibonding level, same energy, constructed in the
z-direction from the 2pz atomic orbitals.) *
antibonding level, same energy, constructed in the
z-direction from the 2pz atomic orbitals.) |
 |






