80-110: The Nature of Mathematical Reasoning
Spring 1998
Class 6: 1/29/98
Definitions II
Mathematical concepts should be defined so that they can be reduced to clear primitive concepts. Sometimes the distance between the concepts and the primitives is far, but once one gets to the bottom things are clear. The following example is meant to be illustrative of the same ideas we have been discussing, but in the context of a real example.
Causation and Probability
The research group I work in spent a decade trying to find the right connections between causal structure and statistical facts. In the end, we developed a theory in just the way I have been discussing. We formulated axioms, we provided definitions, and we proved theorems. The axioms and definitions are relevant for our purpose.
Our goal was to connect causal structure on the one hand, with probabilistic independence on the other. To help, Iíll put causal objects in red font, and probabilistic concepts in green. Here is our fundamental axiom:
Causal Markov Axiom
If G is a causal graph over a set of variables V, and P a probability distribution over V, then for all X Î V, X || V/descendants(X) | parents(X).
Look totally unintelligible? It should, and it will remain so until I provide several definitions to make its claim clear.
The idea is that every variable X is independent of of all of its non-descendants, given its its immediate parents. What are the primitives in this axiom? They are at least:
Lets take causal graph first. Here is its definition:
A causal graph G over V is a directed acyclic graph G over V such that there is an edge in G from X to Y just in case X is a direct cause of Y relative to V.
Now we have to define directed acyclic graph, edge, and direct cause.
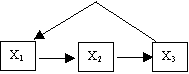
A directed graph G = <V,E> is a set of vertices V and a set of edges E. An edge is an ordered pair: <X1, X2> such that both X1 and X2 are in V, that is, X1, X2 Î V.
For example, the following picture represents a directed graph G:
V = { X1, X2, X3}
E = {< X1, X2>, < X2, X3>}
![]()
An undirected graph is just like a directed graph, but the edges have no order. The same graph as an undirected graph looks like:
![]()
A directed graph is acyclic if there is no path (sequence of arrows) that starts at one vertex and leads back to itself. For example, this graph is cyclic.
Now here I have been sloppy about defining path carefully, but I donít want to drone on forever. Were I to be rigorous, I would have to give a much more careful definition of path.
Parents(X) is the set of all vertices that have arrows in to X.
Descendentss(X) is the set of all vertices V such that there is a path of any length from X to V.
The symbol || stands for probabilistic independence, which I canít cover in detail either. Very roughly, two variables A and B are independent if knowing the value of one doesn't change the probability of the other, i.e., for all values b of B, P(A | B = b) = P(A). For example, suppose A is true if the Steelers go to the Super Bowl in 1999, B is true if nobody fails 80-110, and C is true if Kordell Stewart passes for more than 3,000 yards in 1998-9. A and B are independent, because whether B is true or false doesn't change the probability of A being true or false. A and B are dependent, because Kordell's year has a bearing on A. The construction X || Y | Z, means that X is independent of Y conditional on Z. For example, suppose A is whether or not my 7 year old Katie was exposed to Chick Pox, B was whether or not Katie is actually infected, and C is whether or not she exhibits symptoms. Clearly each pair of these variables are dependent, i.e.,
~(A || B)
, ~(A || C), and ~(B || C). But once you know whether or not Katie is actually infected, whether she was exposed is completely uninformative as to whether she will have symptoms, i.e., A || C | B.Roughly, you now have the definitions you need to understand the fundamental claim of our theory of causality. I have not defined direct cause, but an important feature of our theory is that we donít have to take a stand on how to define direct cause. Define it however you like, but it should connect to probabilistic independence the way the Causal Markov Axiom says it should.
Infinity
Again, mathematical claims do not assert a proposition that can be true or false until their terms are defined. To see this a little more clearly, we will briefly look at some of the paradoxes around comparing the sizes of infinite sets. First, a finite set is a set whose elements could be counted in some definite amount of time. It might be 20 gazillion years, but eventually we would get done. An infinite set goes on and on forever. For example, the natural numbers N = {0,1,2,3 .....} is infinite because we could keep counting forever and never finish.
The first conundrum involves how big a point is. Euclid defined a point as that which has part. What does this mean? He defined a straight line as a line whose points lie evenly. So perhaps it is safe to assume that a line is composed of points. How long is a line? Suppose we define its length as the number of points on it. Then how long is a point?
If a point has zero length, then it seems like no matter how many of them we add together, we will never acumulate any length. Certainly we canít get any length if we add a finite number of 0s together. But if a point has some finite length, even a very small one, e.g., 10-50000 mm, then there will only be finitely many of them on a bounded line, in which case every two lines will have a whole number of points, and thus the ratio of the lengths of any two lines would be expressible as a fraction of two whole numbers, contrary to what the Pythagoreans proved over 2,000 years ago about the ratio of the square root of 2 to 1. So it looks like it has to be zero, and if we want a line to be as long as the sum of the points on it, then we have to somehow find a way to get infinite sums of zeros to total more than zero. That is the solution that modern day measure theory takes to a certain problem we will not go into.
So now if two lines are composed of an infinity of points, and one is longer than the other, then the longer one must have a "bigger" infinity than the smaller one.
![]()
So the infinity of points on the line C-A must be bigger than the infinity of the points on the line B-A. And the inifinity of points on the chord A-B must be bigger than the infinity of points on the chord Aí-Bí in the figure below.
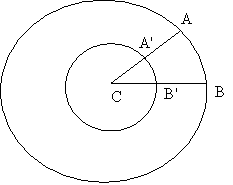
Strangely, however, it is easy to use the radii to construct a 1-1 correspondence between points on the outer circle and points on the inner circle. For example, in the figure above A' can be associated with and A and B' with B, etc. So are the infinities equal or is the circle on the outside a greater infinity? This question cannot be answered until "greater than" is defined clearly, and in a way that it applies to infinite sets.
Related to this is question 4 on the "quiz" I gave out on the first day of class.
Question 4 reads: "there are more whole numbers than there are whole numbers that are odd." We know what whole numbers and odd whole numbers are, but we have not defined "more" for comparing infinite ollections like "odd whole numbers."
We could articulate several candidates for defining "more" for such collections:
1) Collection A has more than collection B if B is properly contained in A, i.e., every member of B is a member of A but some member of A is not a member of A.
2) Collection A has more than collection B if, after proceeding to take one member from A and one from B and throw them out, and repeating this process, we eventually run out of members of B but not of A.
Definition 1 has the problem that two collections that have different sorts of elements cannot even be compared. For example, we couldn't say the set: {1,3,7} had "more" members than the set: {4,6}.
Definition 2 has the immediate problem that if we are comparing two infinite collections, then we will never run out of members of either collection.