80-110: The Nature of Mathematical Reasoning
Spring 1998
Class 11: 2/19/98
1. Formal Logic
We are now going to investigate a theory of mathematical reasoning in which mathematical statements must be in a certain form, so that it is as objective as possible whether or not a supposed proof is in fact valid. In order to make checking validity as mechanical an exercise as possible, we need to be very careful about what sorts of sentences we will analyze.
In Aristotles theory of the syllogism, for example, all sentences must be of the following form:
Quantifier subject predicate.
If a machine could take any sentence of English and identify what is the quantifier, predicate, and subject, then it could also analyze syllogisms for validity. How would a machine parse the following sentence, however:
All of Scheines' classes stink.
The quantifier is obvious, but what about the predicate? Perhaps if it were written:
All of Scheines' classes are courses that stink,
it would be easier to identify things. The sentences are the same, but one is in a form that we can parse into Aristotle's form in an obvious way and one not. Likewise, FOL requires sentences to be in a certain form.
So the first activity is understanding the syntax of FOL, and why it is the way it is.
2. Domains of Discourse, Names, and Constants. nd ourse, Constants,Constants
Mathematical theories usually are about a domain of some sort, e.g., real numbers, rational numbers, geometrical objects, etc. For now, a domain can be though of as a set of objects. To talk about such objects, we need names for them, and since we are building a language that will be formal, we want precise rules for describing the set of names possible.
If the domain is finite, e.g., in Tarski's World, the names can be finite and just listed. A machine can easily check to see if a typed in string is a name by checking it against a list. But if the domain is infinite, like the minutes of time from here to eternity, then no list can be stored in the computer. So instead we must give clear and objective rules for what counts as a legal name and what doesn't. For example, if we wanted to allow only letters followed by numbers, e.g., a32, then a set of rules is the following.
1) If L is a letter, and N a number, then LN is a name.
2) Nothing else is a name.
Or we might write rules that only use the letter "a",
1) If N a number, then aN is a name.
2) Nothing else is a name.
These two definitions allow an infinity of names, but each name is only finitely large. We might want infinitelty large names as well, consisting of any number of letters:
1) All letters are names.
2) If X is a name, and Y is a name, then XY is a name.
3) Nothing else is a name.
In FOL, names that refer to individual objects are called "constants." There are other ways to refer to objects, however. A part of FOL that refers to objects or sets of objects in the domain of discourse are called "terms." One type of term is a name, and another is a function. If I want to construct a sentence in which I say: "the number 3 is odd", then I can do so in the following two ways:
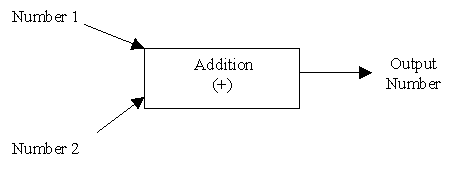
In the second case, I have applied the function "+" to two numbers "2" and "1", and the result is the number 3. It is perhaps helpful to conceive of addition as a function that takes two numbers as inputs and outputs another number:

Since functions take terms and output terms, a functions output can be used as input to another function. For example, the term: (1+1) + 1 is really :
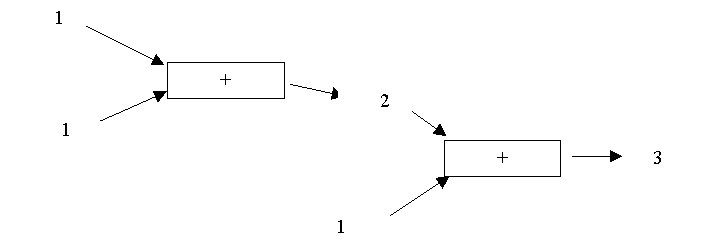
In general, functions take terms as inputs and output another term. The number of inputs may vary, but the output is always 1 term. If there are n inputs to a function F we say that F is an n-place function, or that F takes n arguments.
3. Predicates
Predicates can also be thought of as operators that also take terms as inputs, but that output either true or false instead of another term. For example, the predicate = takes two terms and outputs true just in case they refer to the same object.
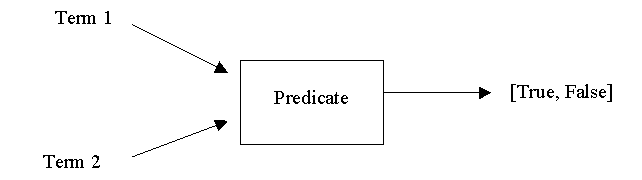
Since a predicate doesn't output a term, it would make no sense to use a predicate's output as input to a predicate, e.g., (2=2) < 3.
-Arity
To form a sentence, predicates go together with a subject, or subjects. For example, the predicate "is an even number" must have one number in front of it before we get a sentence:
7 is an even number.
Some predicates need two numbers before we get a sentence, e.g., the predicate "is larger than"
3 is larger than 4.
Some need three numbers, e.g., "is between"
2 is between 1 and 6.
A predicate that reuqires one object is said to have an "arity" of 1. A predicate that reuqires two objects is said to have an "arity" of 2. A predicate that reuqires three objects is said to have an "arity" of 3., and so on.
When you put together a predicate with the right number of definite objects, you should get a sentence that is true or false. Some predicates are said to be definite, and some vague. For example, the predicate "is an even number" is definite, and the predicate "is smart" is vague. We can give completely clear and permanent rules for the first, but not for the second. In mathematics, only definite predicates get used, and thus we will restrict FOL to involve only definite predicates.