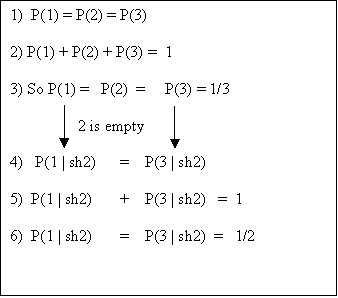
80-110: The Nature of Mathematical Reasoning
Spring 1998
Class 8: 2/10/98
1. Lets Make a Deal Fallacies
Here was the situation you were given in the Lets Make a Deal problem:
Suppose you are on a game show in which there are 3 doors, one of which will contain a terrific prize. The prize is placed behind a door randomly, which means:
P(Prize placed behind door 1), abbreviated P(1), = P(2) = P(3) = 1/3. You are asked to pick a door, but you are not shown what is behind your door. Suppose you pick door 1. Your host (Monty Hall), who knows where the prize has been placed, then shows you one of the doors you did not pick, the only restriction being that Monte must show you a door that is empty. Say you are shown that door 2 does not have the prize. Assuming that you want to pick the door that has the highest chance (probability) of having the prize behind it, having seen that door 2 is empty, do you want to stay with door 1 or switch to door 3?
Another, more general question concerns optimal strategies: Q2) among strategies that either always stay with the original guess, or ones which always switch, which is better, or are they the same?
Here is a series of arguments, each of which seems convincing. Compare them for levels of rigor.
Argument 1: Before you were shown door 2, P(1) = P(3). By showing you the empty door the host has not moved the prize, so he couldn't have changed the chances that the prize is in door 1 or 3, so your chances of winning are equal whether you stay or switch. Since the two must add to 1.0, P(1) = P(3) = .5.
Argument 1 is fallacious, mainly because of an equivocation on what "the chances" mean. Before you were shown door 2, P(1) = P(2) = P(3) = 1/3. These are the pre-game chances. After you are shown that door 2 is empty, you are now considering the chances conditional on being shown that door 2 is empty. Call these the mid-game chances. It is true that the pre-game chances are not changed by Monte announcing that door 2 is empty, but the mid-game chances arenít the same as the pre-game chances. The mid-game, or conditional probabilities are written as, for example, P(1 | sh2), which is to be read as: the probability that the prize is behind door 1, given 2 is empty.
To see that the pre-game and mid-game chances cannot be the same, consider the following argument. After being shown door 2 empty, you know that the prize is behind either door 1 or door 3, and since the probability of exhaustive and exclusive events must add to 1, P(1|sh2) + P(3|sh2) = 1. If P(1) = P(1|sh2) = 1/3, and P(3) = P(3|sh2) = 1/3, then 1/3 + 1/3 must add to one, which is absurd. So the mid-game probabilities can't = 1/3 after you are shown that door 2 is empty. Diagrammicatlly, the argument might look as follows:
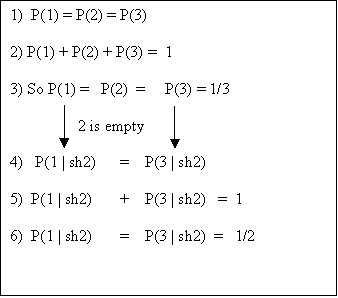
You can see that the move from step 3 to step 4 is fallacious.
Argument 2: Consider two players, M1 and M2. M1 always switches and M2 always stays. If both had picked door 1 to begin with: here is the situation:
M1 - always switch |
M2 - always stay |
|
Prize in door 1 |
Loses |
Wins |
Prize in door 2 |
Wins |
Loses |
Prize in door 3 |
Wins |
Loses |
If each row has probability = 1/3, then M1 wins 2/3 of the time and M2 wins only 1/3 of the time. So switching is always better than staying.
The argument is not rigorous, but is convincing if "switching" refers to the strategy of choosing a door, and then switching to the remaining door no matter what door you are shown, and likewise for staying, but only addresses the second of the two problems we were given. In the first problem we were asked to assess whether we should switch or stay conditional on being shown door 2 is empty. We werenít asked to compare the chances of players who always switched or who always stayed. In fact the middle row doesnít make any sense for player M1, because he canít switch to a door that Monte showed us is empy. A player who always switches doesnít care if he is shown door 2 or door 3 after choosing door 1, he just switches no matter what. Our player might believe that when Monte shows us door 2, the prize is always behind door 3, because he or she believes that if Monte has a choice (the prize is behind door 1), then Monte always picks the higher empty door, so seeing that door 2 is empty is more informative than seeing that door 3 is empty.
Argument 3: In fact, before the game begins P(2 or 3) = 2/3, and after seeing that door 2 is empty P(door 2 or door 3) is still 2/3, but you know it is not in door 2 so P(door 3) = P(door 2 or door 3) = 2/3. So you should switch, because your chances for winning after you switch are twice as high as they would be if you stayed.
This argument is fallacious, in much the same way as argument 1 was fallacious. We say: "after seeing that door 2 is empty P(door 2 or door 3) is still 2/3." It is true that the pre-game chances are still 2/3, but how do we know that the conditional, or mid-game chances are still 2/3? That is, how do we know that P(door 2 or door 3 | door 2 shown empty) = 2/3? We donít.