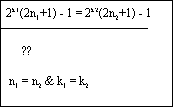
80-110: The Logic of Mathematical Reasoning
Spring 1998
4/28/98
Set Theory - Part 3
Theorem 3: |Q| = |N|
Proof: First we prove the easy half, that |N| ≤ |Q|, and then the harder one: that |Q| ≤ |N|. To prove |N| ≤ |Q|, we need to construct a function F1-1: N ® Q. This is easy, because each natural is also a rational, so we can use a version of the identity function: f(n) = n/1.
F = {<n,<n,1> | n Î N}. To prove |Q| ≤ |N|, we need to construct a function
G1-1: Q ® N. Consider the following function: g(k,n) = 2k(2n+1) - 1.
What might be wrong with this function? It might not be defined for some rational, it might return a value not in N, and it might not be 1-1. Lets consider each in turn. Since 2k is defined for any natural number k, and so is 2n, it certainly returns some number for every rational <k,n>. Might one of these numbers not be in N? Might it be a negative number, or not a whole number? The smallest that 2k can be is 1, because 0 ≤ k. The smallest 2n can be is 0, and thus 2n+1 is at least 1, and thus 2k(2n+1) must be at least 1, so g(k,n) is never negative. Is this function 1-1? Lets apply the definition of 1-1 to this function and see.
G is a 1-1 function from A to B « " <a1,b1>,<a2,b2>Î G[ a1 = a2 « b1 = b2]. In this case that translates into:
"
<<k1,n1,>,2k1(2n1+1) - 1>, <<k2,n2,>,2k2(2n2+1) - 1>Î G[ (n1 = n2 & k1 = k2) « (2k1(2n1+1) - 1 = 2k2(2n2+1) - 1)].
It should be obvious that (n1 = n2 & k1 = k2) ® (2k1(2n1+1) - 1 = 2k2(2n2+1) - 1). So all the work is in establishing that: (2k1(2n1+1) - 1 = 2k2(2n2+1) - 1) ® (n1 = n2 & k1 = k2).
Lets do this with natural deduction style proofs, just like we did in class for the section on sentential logic. Beging with this statement on the bottom of the page as a goal, and work backwards. It is a conditional sentence, so we can assume the antecedent and try to prove the consequent:
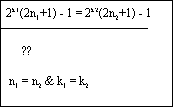
Now lets work forwards a little from the assumption. Add 1 to both sides in the first step, and divide both sides by 2k1 and then 2n2+1 in the second:
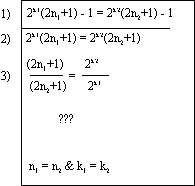
Now lets work backwards, in which case our goal is n1 = n2 & k1 = k2. This is a conjunction, so lets use conjunction introduction to split it up into two goals:
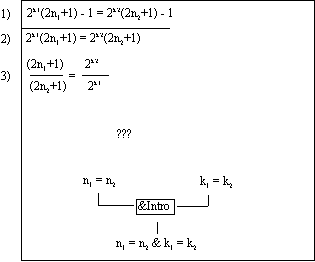
Lets try to prove k1 = k2 first. This is atomic. We can’t build it with introduction rules. It is not embedded above, so lets go indirect, and try a reductio ad absurdum:
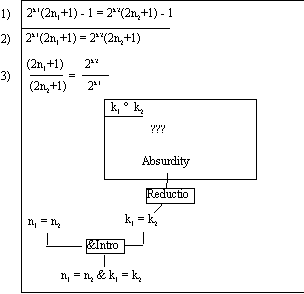
This leaves us with the task of figuring out an absurdity (contradiction) to prove. Work forward with the assumption just introduced: k1 ≠ k2. If k1 ≠ k2 then either
k1 > k2 or k1 < k2. Now we can use argument by cases:
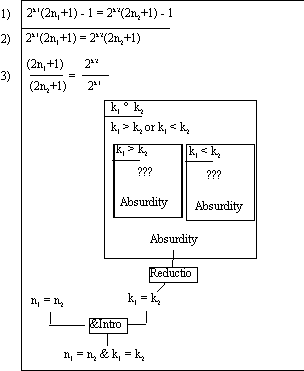
In the righthand subproof, in which k1 < k2, line 3 is available. From the right side of the equation, we know that 2k2 is even, and 2k1 is either a smaller even number or 1. In either case the right hand side of the equation on line 3 is an even number. But both the numerator and denominator on the left hand side of equation 3 are odd, and so the left hand side of equation 3 is odd. But an odd cannot equal an even, so we have derived an absurdity:
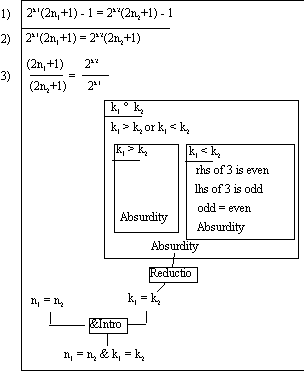
If we flip the numerator and denominator on each side of the equation in line 3, then we can produce an analgous argument for the case where k1 > k2. Now we know that k1 = k2, so we can use it in proving that n1 = n2. But now look at the equation in line 3 again, and you will see that the right hand side must equal 1, so 2n1+1 = 2n2+1, from which it is immediate that n1 = n2. Q.E.D.
We have proved that the rationals are no bigger than the naturals, even though there are an infinity of rationals between every two natural numbers. But recall that in the very first week of class we proved that there is a number that cannot be expressed as a rational, namely Ö 2. So even though we can find a rational q1 arbitrarily close to Ö 2 but less than it, and one that is arbitrarily close to it but greater q2, and then an infinity of rationals between q1 and q2, we can never exactly hit Ö 2. So there are still holes in the rationals! Next class we consider the Reals, which include the rationals and their holes, and show that there are more Reals than rationals.