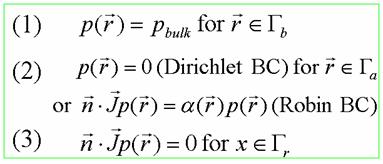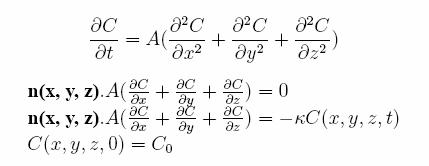|
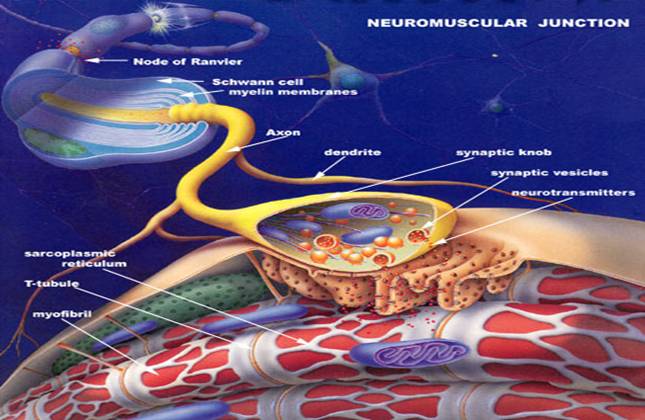
Multi-Scale Modeling of Neuro-Muscular Junction (NMJ)
|
|||
|
1.
Objective In this project, we want to construct
multi-scale models for the neuro-muscular junction
(NMJ) system, and calculate the electrostatic potential and diffusion rate constant
by solving corresponding partial differential equations (Possion-Boltzmann
equation and Smoluchowski equation).
http://fig.cox.miami.edu/~cmallery/150/neuro/neuromuscular-sml.jpg |
|||
|
2.
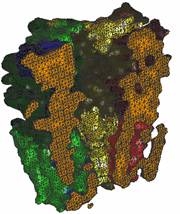
Modeling We first construct volumetric data from PDB
data or the input geometry, then use our LBIE_Mesher
software (Level Set Boundary Interior and Exterior Mesher)
to generate adaptive and quality tetrahedral meshes for each components in
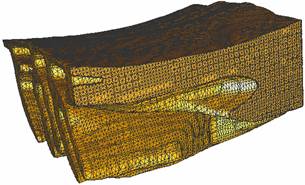
the NMJ system. 2.1 Membrane |
|||
|
|
|
||
|
|
|
||
|
Interior mesh (224475 vertices, 1077728 tetrahedra) |
Exterior mesh (74299 vertices, 374524 tetrahedra) |
||
|
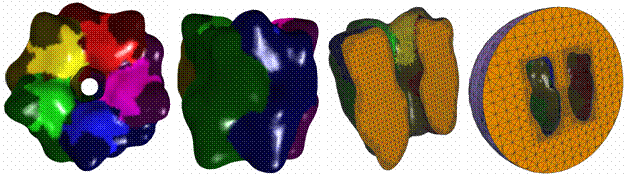
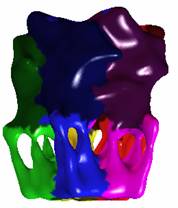
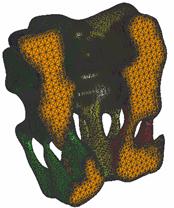
2.2
AChBP (1I9B) – the top part of AChR |
|||
|
|
|||
|
Blobbiness
= -0.5, interior mesh (106971 vertices, 527438 tetra), exterior mesh (113528
vertices, 559670 tetra). |
|||
|
|
|||
|
Blobbiness
= -0.1, interior mesh (77110 vertices, 381280 tetra), exterior mesh (109438
vertices, 560535 tetra). (download
interior/exterior tetra meshes) |
|||
|
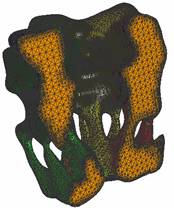
2.3
AChR – Receptor |
|||
|
|
|||
|
Blobbiness = -0.5 |
|||
|
|
|||
|
Blobbiness = -0.1 |
|||
|
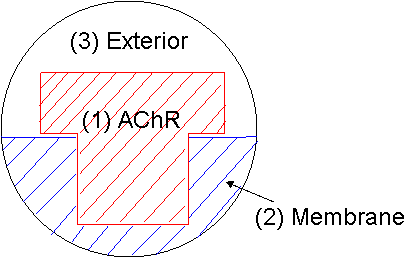
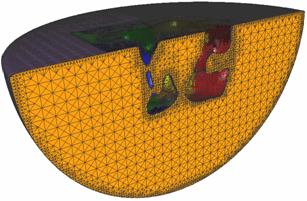
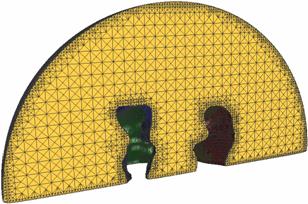
2.4
A model of an AChR
and membrane (small local region) within a sphere |
|||
|
|
|||
|
|
|
|
|
|
(1) AChR |
(2) Membrane |
(3) Exterior |
|
|
|
|||
|
3. Simulation |
|||
|
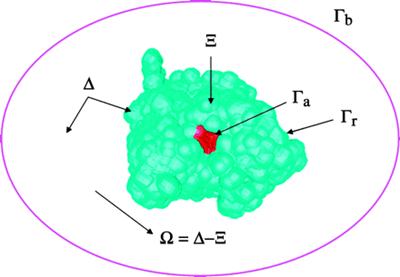
3.1 Possion-Boltzmann Equation – to calculate the electrostatic potential The Possion-Boltzmann
equation (PBE) determines a dimensionless potential u(x) = ecФ(x)/(kBT)
around a charged biological structure immersed in a salt solution, where Ф(x) is the electrostatic
potential at
Where References: 1. Holst M, Baker N, Wang F. Adaptive multilevel finite
element solution of the Poisson-Boltzmann equation
I: algorithms and examples. J. Comput. Chem.
21, 1319-1342, 2000. 2. Baker N, Holst M, Wang F.
Adaptive multilevel finite element solution of the Poisson-Boltzmann equation II: refinement schemes based on
solvent accessible surfaces. J. Comput. Chem.
21, 1343-1352, 2000. 3.2 Smoluchowski Equation – to calculate the diffusion-influenced biomolecular reaction rate constant The Smoluchowki equation describes the overdamped dynamics of multiple particles while neglecting interparticle interactions. For a stationary diffusion process, the Smoluchowski equation has the steady-state form of
Where Lp(x) represents (dp(x, t)/dt) (t is the time), p(x) is the distribution function of the reactants, D(x) is the diffusion coefficient, β = 1/kT is the inverse Boltzmann energy, k is the Boltzmann constant, T is the temperature, and W(x) is the potential mean force (PMF) for the diffusing particle.
References: 1.
Y. Song, Y.
Zhang, T. Shen, C. Bajaj,
J. McCammon, N. Baker. Finite Element Solution of the Steady-state Smoluchowski Equation for Rate Constant Calculations.
Biophysical Journal, 86(4):2017-2029, 2004. 2.
Y. Song, Y.
Zhang, C. Bajaj, N. Baker. Continuum Diffusion Reaction Rate Calculations of
Wild Type and Mutant Mouse Acetylcholinesterase:
Adaptive Finite Element Analysis. Biophysical Journal
87(3):1558-1566, 2004. 3.
D. Zhang, J. Suen, Y. Zhang, Y. Song, Z. Radic,
P. Taylor, M. J. Holst, C. Bajaj,
N. A. Baker, J. A. McCammon. Tetrameric Mouse Acetylcholinesterase:
Continuum Diffusion Rate Calculations by Solving the Steady-State Smoluchowski Equation Using Finite Element Methods.
Biophysical Journal 88(3):1659-1665, 2005. 3.3 Particle Diffusion Equation - to model the diffusion of neurotransmitters across the synaptic cleft The Reaction Diffusion Equation is used to model the diffusion of particles across a domain. This is given by the following equation with boundary and initial conditions:
Where: C (x,y,z,t) = concentration of the Neurotransmitters at a given time C0 = initial concentration at time t=0 n(x,y,z) = surface normal kappa = specific reactivity A = Diffusion Reaction Coefficient |
|||
|
|
|||