Structural Test #3:
Analysis of a 3D solid object
Introduction:
In this
test problem you will be required to test your knowledge of 3D modeling
and the Solid element in ANSYS.
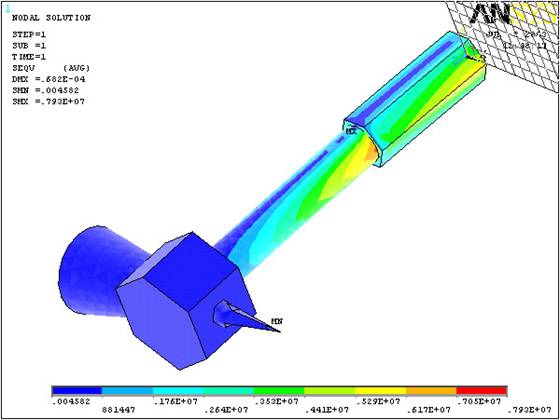
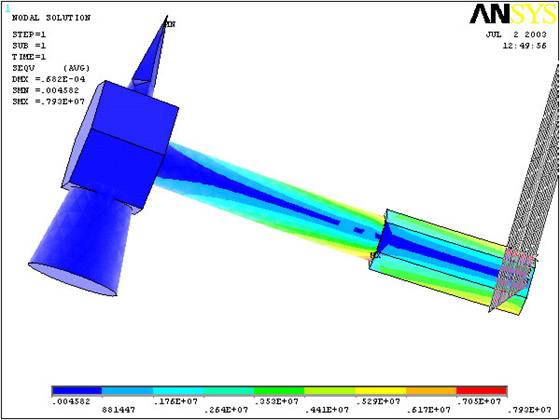
Physical Problem: One
day while using his hammer, Professor Shimada attempts to drive a nail
into the floor of his home. Unbenounced to
him a layer of pure steel had been installed under the wooden floor.
The nail doesnít move and so a point force of 100N is exerted on the
head of the hammer. Plot the nodal solution of the deformation and
stresses on the hammer.
Problem Description:
 |
We will model the
object using solid Tetrahedral 10 node element. |
 |
Material:
Assume the structure is made of steel with modulus of elasticity E=200
GPa and a
Poisonís Ratio of 0.3. |
 |
Boundary conditions:
The hammer is fixed at the base..
|
 |
Loading:
The object is has a point force of 100N at the head. |
 |
Objective:
 |
To plot deformed
shape. |
 |
To determine the
principal stress and the von Mises
stress. (Use the stress plots to determine these. Do not print the
stress list) |
 |
What is the
maximum load the object can take. Clearly
mention the yield stress that you have assumed for steel. Also
assume factor of safety of 1.25. |
|
 |
You are required to
hand in print outs for the above. |
 |
Figure: |


 |
Dimensions:
|
10 cm
hexagonal handle, radius 0.02m, theta=300 at (0,0)
15 cm
circular solid, radius 0.015m at 0,0)
5 cm
hexagonal head joint, radius 0.04m, theta=270 at (0,0)
18 cm top cone, radius=0.03m
 |
Create the hexagonal solid defining the grip for the handle.
|
 |
Shift
the workplane the axial length of the
hexagonal solid and create the circular solid defining the section
between the handle and the head of the hammer. |
 |
Shift
the workplane again and create the
hexagonal head of the hammer. |
 |
Now
rotate the workplane and shift it such
that the cone is created 0.09m in the correct direction from the axial
center of the handle. |
 |
Now
overlap the conic section and the hexagonal volume defining the head
of the hammer. Once these are married into one volume,
add the volumes together such that the
hammer is one full volume. |
 |
Define the Material
Properties of the Steel hammer (Elastic Modulus and Poisonís
Ration are the important qualities) |
 |
Define the Element
Properties as a Tet 10 node Structural Solid. |
 |
Mesh the hammer.
(Do so by picking all lines and setting the element edge length to
0.01.) |
 |
Apply the boundary
conditions. (Structrual Displacement on
the bottom face of the handle equal to
zero, and a structural force / moment on a node closest to the center
of the hammer head as possible equal to 100N in the X direction. If
the hammer head is oriented properly then this value should be
directed perpendicularly into the face of the hammerís head.)
|
 |
Solve |
 |
List the nodal
results of the solution with respect to all degrees of freedom.
|
 |
Plot the nodal
solution with respect to all degrees of freedom. Show both the
deformed and undeformed shape of the
hammer. |
(The
output should be identical to the figure below)
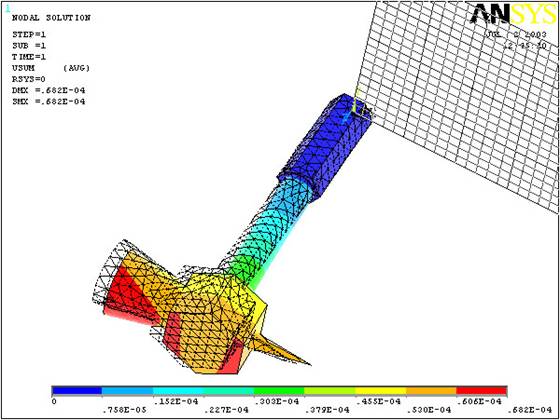
(Without the Undeformed Hammer it should
look like this:)
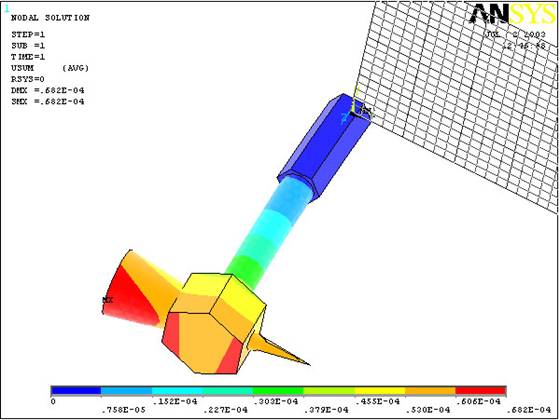
(Select
a stress (say von Mises) to be
plotted and click OK. The output will look like this.)