ADAMS Labs: Simple Pendulum
Introduction:
Problem:
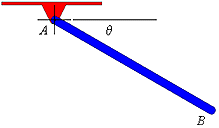
| AB is a uniform bar with a mass of 2 kg and a length of 450mm.
Bar AB swings in a vertical plane about the pivot at A. The
angular velocity (theta dot) = 3 rad/s when theta = 30 degrees. Compute
the force supported by the pin at A at that instant. |
 |
This problem is asking for the force supported by the pivot A at an
instant when the 2 kg bar is 30 degrees from the horizontal and has an
angular velocity of 3 radians per second. We will use ADAMS to create a
model with the given conditions and obtain the data needed.
Procedure:
1.1. Starting ADAMS.
- From the ADAMS product menu, select ADAMS.
The Run ADAMS dialog box appears.
- Select OK.
The Welcome to ADAMS dialog box appears as shown in Figure 1.
- Under the heading "How would you like to proceed", select
Create a new model.
Verify the Gravity text field is set to Earth Normal (-Global Y).
Verify that the Units text field is set to MMKS - mm,kg,N,s,deg.
Select OK.
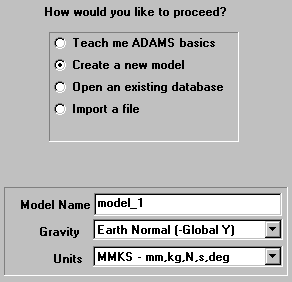 Figure 1. Welcome
to ADAMS. Figure 1. Welcome
to ADAMS. |
1.2. Making the bar.
- Click on the parts palette in the Toolbox with the right mouse button.
The button stack for parts appears.
- Select the Rigid Body: Link tool.
 with the left mouse button.
with the left mouse button.
- In the link container at the bottom of the Toolbox, activate the Length
toggle switch and enter 450mm in the text field below.
- Activate the Width toggle switch and enter 20mm in the text
field.
- Activate the Depth toggle switch and enter 27.5mm in the text
field.
- Click once with the left mouse button on the point (-225,0,0) to select
the starting point and click once with the left mouse button anywhere right
of the start point along the global x-axis to select the direction.
ADAMS will create and display the bar. The display should appear similar
to Figure X below.
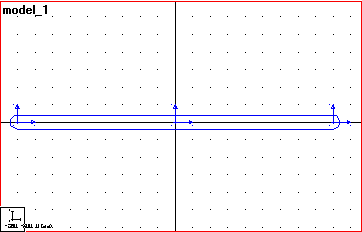 Figure X. Link
Figure X. Link
1.3. Setting the mass of the bar.
The problem specifies that the bar has a mass of 2 kg. ADAMS automatically
calculates the mass properties based on the material and the geometry,
but in this case, it can be set manually since the mass of the bar is given
as an initial condition.
- Click on the bar with the right mouse button. Follow the pull-right
menu for Part:PART_1 and select Modify.
The Modify Rigid Body dialog box appears.
- In the Mass & Inertia defined by: entry, use the pull down
arrow to select User Input.
An alert box may open. Click on Close.
- In the Mass text field of the Modify dialog box, type in 2.0
and click OK.
The mass of the bar is now set at 2 kg.
Note: Due to the way the geometry was defined, the mass of the bar is
already very close to 2 kg, so we can assume no inertial properties need
to be changed.
1.4. Setting the position of the bar.
- To set the angle of the bar at 30 degrees, click on the Position
icon
 in the Toolbox.
in the Toolbox.
- Enter 30 in the Angle entry and select the bar so it is highlighted.
- Click on the clockwise arrow once.
The bar is now at a 30 degree angle from horizontal.
1.5. Creating a pivot.
- Click on the Joint icon in the Main Toolbox and select the Joint:Revolute
icon
 from the joints button stack.
from the joints button stack.
- Verify that the Construction text field reads 1 Location
and Normal to Grid.
- Position the cursor over the marker MAR_1 at the left end of
the bar and click once with the left mouse button.
- A joint between the bar and the ground is created at that location.
1.6. Setting initial motion.
All of the parts have now been created and the constraints added. The
next step is to add an initial motion to the revolute joint that specifies
a starting rotation rate of two radians per second.
- Click and hold the bar with the right mouse button and follow the pull
right menu for Part:PART_1 and select Modify.
- Click on the Velocity ICs button to open the Settings dialog
box.
- Under the heading Initial angular velocity about:, select Part
CM.
- Below that, click on the Z axis selection box and enter 3.0r,
for 3.0 radians per second, in the text field that appears next to it.
- Click on Apply and close the window.
- Click on Ok in the Modify window.
1.7. Verify the model.
The model verification step is one way to find errors in the model definition.
ADAMS checks for error conditions such as misaligned joints, unconstrained
parts, or massless parts in dynamic systems, and alerts you to other possible
problems in the model.
- In the lower right corner of the modeling window, click on the Information
icon
 with the right mouse button.
with the right mouse button.
The information palette appears.
- Click on the Verification icon.

The Info Window appears.
- After seeing that the model has verified successfully, click on the
Close button in the upper right corner to close the Information Window.
The completed model should appear similar to Figure X below:
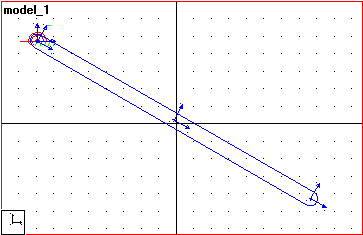 Figure X. Completed
pendulum model. Figure X. Completed
pendulum model. |
Model building is now complete.
Set up and run a simulation.
1.8. Setting measure for the force supported by the pivot at point
A.
- Click on the revolute joint at the upper left end of the bar with the
right mouse button and follow the pull-right menu for Joint:JOINT_1
and select Measure.
The Joint Measure dialog box opens.
- Select Force for the Characteristic entry and mag
(magnitude) for the Component entry.
- Click OK.
A graph window appears. This is where the reaction force will be displayed
during the simulation and animation.
1.9. Running the simulation.
- Click on the Simulation icon
 in the Toolbox. For End Time, enter 0.5 and for Steps,
enter 50.
in the Toolbox. For End Time, enter 0.5 and for Steps,
enter 50.
- Click on the Play icon.

You should see the bar swing about the pivot and corresponding data should
be plotted on the JOINT_1_MEA_1 graph.
- When the simulation ends, click on the Rewind icon.

1.10. Find the force supported by the pivot.
- Click on a blank area inside the small plot window with the right mouse
button and follow the pull right menu. Select Transfer to Full Plot.
The ADAMS Plot Window will open, replacing the Modeling window.
- Now go to the Plot Window and select the Display Plot Statistics icon.

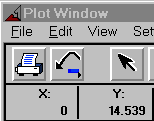
Since we know the initial conditions are met at the start of the simulation,
move the cursor over the starting point of the plot.
- At the top of the window, X will be displayed as 0 and Y, which is
the force on the pivot, will be displayed. That is your answer.
Compare it to the results given in the Solution section of this
Lab.
- To return to the modeling window, go to the File pull-down menu
and select Return to Modeling.
1.11. Saving your Modeling Session.
- Under the File pull-down menu, select Save Database As...
The Save Database As dialog box appears as shown in Figure X.
- In the text field next to File Name, enter the name you wish
to give this model, for example, pendulum.
- Select OK.
An ADAMS Binary File is created.
1.12. Exiting ADAMS.
- Select Exit from the File pull-down menu in the main
ADAMS Modeling window.
Congratulations, you have completed ADAMS Lab: Pendulum.
Solution:
- The force supported by pivot A is 14.5 N.

- Here are the results from my ADAMS simulation:
Download the ADAMS command file for this model: pendulum.cmd
Did it work?
If the instructions were followed correctly, your ADAMS results should
match the results shown above. The correlation to the analytical solution
can be improved by decreasing error tolerance and recommuting the analytical
results using more decimal places. The close correlation should provide
confidence in your ability to create models using parts with initial velocities
and joints and ADAMS' ability to solve them.
- Make sure correct units are set to mmks.
- Make sure gravity is on and in the -Y direction and set
to 9806.15.
- Make sure the revolute joint is in the z direction.
- Check dimensions of the part to make sure they are correct.
- Check mass properties to make sure they are correct.
- Check orientation of the part to make sure it is correct.
- Make sure the measure is set to the magnitude of the reaction force.
- Make sure the plot is displaying the correct set of results.

 Figure 1. Welcome
to ADAMS.
Figure 1. Welcome
to ADAMS.  Figure X. Link
Figure X. Link  Figure X. Completed
pendulum model.
Figure X. Completed
pendulum model.