Return to lecture notes index
March 23, 2010 (Lecture 17)

Error Detection and Correction

Data in transmission is rarely perfectly safe. Transmitting data subjects it to interference. Occasionally the data gets corrupted along the way. Corrupted data is very hard for application software to manage -- it can't reasonably be expected to check every single piece of data for errors before using it. So, we take care of this within the network software.

The basic idea is that we break the data into pieces, known as frames. To each of these frames, we add some additional information -- Error Detection Codes (EDCs) or Error Correction Codes (ECCs). These extra bits will enable us to detect and or correct most failures.

In either case, sending these extra bits wastes some network time, so we like to keep them to a minimum, thereby spending most of our time sending the actual data. And, ECCs are larger than EDCs, so we use them sparingly. In fact, we generally only use ECCs in storage systems, e.g. disk drives, or in particularly error-prone but high-bandwidth media, e.g. satellites. Otherwise, we use only EDCs, because we can often resend the data on the rare occasions that it becomes corrupted in transmission.

In summary, by adding ECCs to data, we gain the ability to correct some errors. By adding EDCs, we gain the ability to detect some errors -- but we are unable to correct them, so our recourse is to discard the frame.

Visualizing Error Correction and Error Detection

Imagine that we want to send a message over the network. Our message is either a) RUN or b) HIDE. We could very efficiently encode these messages as follows:

But, the problem with this encoding is that if a single bit gets flipped, our message is undetactably corrupted. By flipping just one bit, one valid codeword is morphed into another valid codeword.

Now, let's consider another encoding, as follows:

The 2-bit encoding requires twice as many bits to send the messages -- but offers more protection from corruption. If we, again, assume a single-bit error, we still garble our transmission. Either "00" or "01" can become "01" or "10". But, neither can, in the case of a single bit error, be transformed into the other. So, in this case, we can detect, but not correct the error. it would take a two bit error for the error to become an undectable Byzantine error.

Now, let's consider a 3-bit encoding, which takes three-times as much storage as our original encoding and 50% more storage than our encoding which allowed for the detection of single-bit errors:

Given the encoding above, if we encounter a single bt error, "000" can become "100", "010", or "001", each of which is 2-bits from our other valid codeword, "111". Similarly, should a transmission of "111" encounter a single-bit error, it will become "011", "101", or "110" -- still closer to "111" than "000".

The upshot is this. Since single-bit errors are much more common than multiple bit errors, we correct a defective codeword by assuming that it is intended to be whatever valid codeword happens to be closest to it as measured in these bit-flips. If what we have doesn't match any codeword, but is equally close to more than one codeword, it is a dectable, but uncorrectable error.

Hamming Distance

In the examples above, I measured the "distance" between to codewords in terms of the number of bits that one would need to flip to convert one codeword into the other. This distance is known as the Hamming Distance.

The Hamming Distance between two codes (not individual codewords) is the minimum Hamming distance between any pair of codewords within the code. This is important, because this pair is the code's weak link with respect to error detection and correction.

This is a useful measure, because as long as the number of bits in error is less than the Hamming Distance, the error will be detected -- the codeword will be invalid. Similarly, if the Hamming distance between the codewords is more than double the number of bits in the error, the defective codeword will be closer to the correct one than to any other.

How Many Check Bits?

Let's consider some code that includes dense codewords. This would, for example, be the case if we just took raw data and chopped it into pieces for transmission or if we enumerated each of several messages. Given this situation, we can add extra bits to increase the Hamming distance between our codewords. But, how many bits do we need to add? And, how do we encode them? Hamming answered both of these questions.

Let's take the first question first. If we have a dense code with m message bits, we will need to add some r check bits to the message to put distance between the code words. So, the total number of bits in the codeword is n, such that n = m + r

If we do this, each codeword will have n illegal codewords within 1 bit. (Flip each bit). To be able to correct an error, we need 1 more bit than this, (n + 1) bits to make sure that 1-bit errors will fall closer to one codeword than any other.

We can express this relationship as below:

Hamming's Code

Hamming offered an encoding that illustrated the lower limit described above. This code allows the correction of 1-bit errors (but not the detection of 2-bit erros). The encoding works as follows:

Hamming Code: Example Encoding

Let's consider encoding the message "1100001". Notice that we'll use the power-of-two bits for the extra check bits. 

  _    _     1   _    1    0    0   _    0   0   1
  1    2     3   4    5    6    7   8    9   10  11

So, the message that we send of the network is as follows: 

  1    0     1    1     1     0    0   1    0   0   1
  1    2     3    4     5     6    7   8    9   10  11

Hamming's Code: Correcting a 1-Bit error

Given the code above, what happens if we encounter a 1-bit error? Consider the following: 

  Intended Message:  1    0    1    1    1    0    0   1    0   0   1
  Corrupted Message: 1    0    1    1    1    0    1   1    0   0   1

Visually, we can see that bit-7 is in error. But, how can we determine this algorithmically? We recalculate the parity associated with each of our groups: Bit-1's group, Bit-2's group, Bit-4's group, and Bit-8's group:

So, let's consider the example above:

It is worth noting that Hamming codes can be precomputed and placed into tables, rather than being computed on the fly.

Cyclic Redundancy Check (CRC)

Perhaps the most popular form of error detection in netowrks is the Cyclic Redundancy Check (CRC). The mathematics behind CRCs is well beyond the scope of the course. We'll leave it for 21-something. But, let's take a quick look at the mechanics.

Smart people develop a generator polynomial. These are well-known and standardized. For example:

These generators are then represented in binary, representing the presence or absence of each power-of-x term as a 1 or 0, respectively, as follows:

In order to obtain the extra bits to add to our codeword, we divide our message by the generator. The remained is the checksum, which we add to our message. This means that our checksum will have one bit fewer than our generator --= note that, for example, the 16-bit generator has 17 terms (16-0). Upon receiving the message, we repeat the computation. If the checksum matches, we assume the transmission to be correct, otherwise, we assume it to be incorrect. Common CRCs can detect a mix of single and multi-bit errors.

The only detail worth noting is that the division isn't traditional decimal long division. It is division modulus-2. This means that both additon and subtraction degenerate to XOR -- the carry-bit goes away.

Let's take a quick look at an example: 

                        1 1 0 0 0 0 1 0 1 0 
                ________________________________ 
   1 0 0 1 1    |    1 1 0 1 0 1 1 0 1 1 0 0 0 0 
                     1 0 0 1 1
                     ---------
                       1 0 0 1 1
                       1 0 0 1 1 
                       ---------
                                 1 0 1 1 0
                                 1 0 0 1 1
                                 ---------
                                     1 0 1 0 0
                                     1 0 0 1 1 
                                     ---------
                                         1 1 1 0   <------This is the checksum

A Second Look At Framing

At the beginning of today's conversation, I mentioned that we carved messages into small chunks known as frames. Now that we've discussed error correction, we can discuss framing a bit further.

Framing is essential for the management of network communication. We need to cut data into pieces in order that we can label it with checksums for error correction and detection. We also need manageable pieces should we need to discard and possibly resend a chunk.

So, what should be the frame size? Well, this depends on the data rate and the error rate. The higher the error rate, the small the frame. The reason is simple -- if we have a large frame and have to throw something away, we'll end up throwing out more. If we have an error rate of one bit per million and our frame size is a ten-million bits, we'll virtually never get to send the frame -- each attempt will have, on average, 10 errors. But, if the frame size is 1,000 bits, almost all of the frames will go through without error.

So, why not have very small frames, need it or not? Well, frames typically contain non-data. For example, they usually have special "framing bits". These bits make it possible to resynchrnoize with the beginning of the frame if bits are lost or injected into the stream, such as by a bad buffer in a network switch. Frames might also contain other non-data, such as a frame-number for retransmission, or the protocol number for the higher-level protocol, etc. As a result, smaller frames usually result in a greater percentage of the network time spend sending metadata (non-data overhead), rather than the payload (the user data). More frames means more frame headers, etc.

By the way, in class, someone asked what happens if the framing pattern occurs within the payload. The answer is that it usually needs to be escaped.

The Point-To-Point (PPP) Protocol Example

Just to show you guys a real-world example, below is the structure of the frame used by the Point-To-Point (PPP) protocol: 

  Flag         Address        Control    Protocol    Payload    Checksum      Flag
  8-bits       8-bits         8-bits     8/16-bits   varibale   16/32-bits    8-bits
  01111110     11111111       00000011                                        01111110

Notice the bits pattern used to delimit the begining and ending of the chunk of data, e.g., frame the data.

In the case of PPP, the address bits are almost always all 1s, as it is almost never used, except as a point-to-point protocol with only two stations, not as a multi-station broadcast protocol. The control bits are usually as shown, but can also be used to number frames and a reliable protocol. As it turns out, the sender and receiver can agree, during the initial negotiation, to leave both of these often-unused fields out of the frames, reducing the non-data overhead.

Failure and Storage

Now that we have discussed error-correction and error detection codes and their applicability to data communication, we're going to talk a little bit about reliability and storage.

In discussing EDCs and ECCs, as used in communications, we said that ECCs are very rarely used. Instead, the most common approach is simply to resend the data, if appropriate. The only exception we carved was in intrinsicly noisy, but high-bandwidth channels, such as satellites. In these cases, ECCs make sense, because they enable us to make use of a media that, otherwise, might be too noisy to use.

But, when it comes to storage systems, such as disks, ECCs are an intinsic part of the system by design. If we lose the data, we can't just go back to the well. There is nowhere to go.

And, as it turns out, modern disks are technological marvels obtaining a tremendous information density at tremendous speeds by pushing the media and the technology right to its tolerances. Getting a bit wrong here or there isn't tremendously rare -- disks regularly use ECCs to deliver data. ECC logic is built directly into the controllers and is applied with every read and write.

It is worth noting that, in addition to protecting against read/write problems, good storage systems protect against power failure, cabling failure, human error, &c.

Failure and Scale

In the real-world many devices experience a "bath tub" like failure model. The highest rate of failure is dead-on-arrival units and those that failure during a burn-in period. So, we start out with a high failure rate that quickly drops off to a low, stable rate of failure, where it remains for years. But, eventually, as the devices age, failures cease being rare. Once the failure rate increases, it seems to hang out in this final phase of aging, a steadily, but slowly increasing failure rate, until the last of the units die.

But, for the purpose of this discussion, let's ignore this common, real-world failure model and do some really broken, but simple, math. Suppose the mean time between failures (MTBF) of the average disk is 50,000 hours -- about 6 years. Now imagine that we have 100 disks in service. We can expect a failure every 500 hours: 1 failure/50,000 hours/disk * 100 disks = 1 failure/100 hours. So, we now expect a failure every few weeks.

Even if this is over simplified, it does highlight the fact that as the quantity scales up -- so do failures. Beyond a certain point, failure is the steady-state, not the exception. Any system that operates beyond a certain scale must be designed to work each and every day with failed components. I honestly doubt that the Googles of the world bother to replace things as they break. I suspect that they just let them fail and replace them only when it is time for an upgrade or a whole rack of components fail or the sprinkler system accidentally gets turned on, I dunno'.

So, this portion of the lecture is basically a case study in managing failure -- RAID arrays. They were once an extravagance in high-end systems, but are now the backbone of performance and reliablity in even modest configurations. Let's take a look at how they use redundancy to achieve reliability and performance, despite scale.

Redundant Arrays of Independent (formerly, Inexpensive) Disks (RAID)

The goal of most RAID systems is to improve the performance of storage systems. The idea is that, instead of building/buying more expensive disks, we can use arrays of commodity disks organized together to achieve lower latencies and high bandwidths.

But, as we scale up the number of disks required to store our data, unless we do something special, we'll also scale up the likelihood of us losing our data due to failure. So, what we are actually going to discuss is how to organize disks to achieve better performance (lower latency and/or higher bandwidth) as well as greater reliability (fail-soft or fail-safe).

RAID - Striping

RAID systems can obtain increased bandwidth by distributing data across several disks using a technique is called striping. The result of this technique is that the bandwidth is not limited by a single drive's bandwidth, but is instead the sum of the bandwidth of several drives.

When we think about I/O with RAIDs, we don't think in terms of sectors or blocks. Instead we think about stripes A stripe is an abstraction that represents the fundamental unit of data that can be written simultaneously across several disks. The amount of data that can be stored in a stripe is called the stripe width. A portion of the stripe is stored on each of several disks. This portion is caled the stripe unit. The size of the stripe unit is the number of bytes of a stripe that are stored on a particular disk.

If the stripe width is S bytes and we have N disks available to store user data, the strip unit is S/N bytes. For example, if a RAID has 5 disks available to store user data, and the stripe width is 100K, each stripe unit is (100K/5) 20K.

If the application or OS I/O buffer cache reads an entire stripe at a time, the array controller can perform parallel accesses to all N disks. The bandwidth as viewed by the user is not the bandwidth of each individual disk, but is instead the aggregate bandwidth accross all disks.


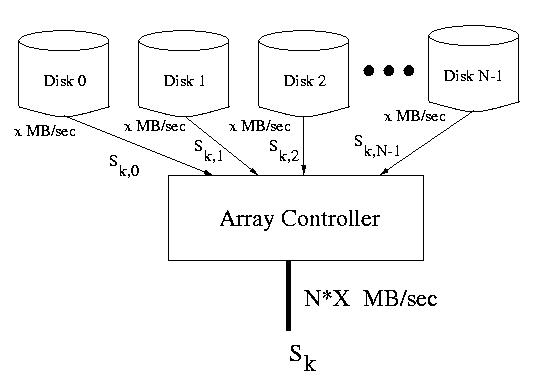
Figure: An entire stripe delivered at once from several disks at N * X MB/sec

If several requests are made concurrently, it may be possible to service all or some of them in parallel. This is because requests for data living in strip units on different disks may be performed in parallel. In this way the array can service multiple requests at the same time. Of course, if the requests live in stripe units on the same disk, the requests must still be serialized.


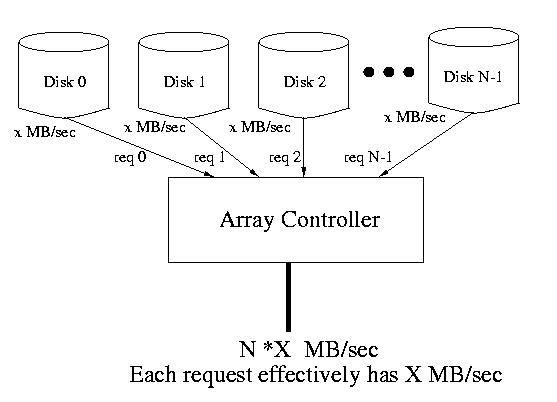
Figure: N requests serviced at once from N different disks each at X MB/sec

If we hold constant the number of disks available for user data, we can tune the performance of the array by varying the stripe unit size:

Many commercially available arrays allow the administrator to select from several available stripe unit sizes when the disk is first initialized. Other arrays are not configurable, so this becomes a purchase-time consideration.

Improving Reliability

In order to improve the reliability of these arrays, we'll make use of redundancy. In particular, we'll either mirror a copy of the data directly to a redundant disk, or we'll add parity or other error-correction codes to the system that enable us to recover from disk failure.

It is important that, at this point, we are discussing parity across disks that enables us to recover from the complete failure of an entire disk, rather than the incorporation of ECCs into a single disk, which enable the recovery of small amounts of corrupted data on an otherwise functioning disk.

RAID Approaches

There are many approaches to achieving the redundancy required in arrays. Although there are other classifications, most commercial RAIDS fall into categories known as levels: RAID level 1 - RAID level 6.

There are several metrics that can be used to evaluate alternatives:

RAID Level 1

Raid level 1 is also known as Mirroring. Disks within the array exist in pairs -- a data disk and a corresponding backup disk. Blocks can be read from either disk in the pair, but in the normal case, data is always written to both disks. Depending on the assumptions about the types of failure, the writes to the data and backup disks may or may not be performed in parallel.

In the event of a failure, data is read and written to and from the working disk. After the defective disk is replaced, the data can be reconstructed from its twin.

It is also possible to locate the mirror disks miles and miles apart. This insulates the data from a location-induced failure like an earthquake, flood, or fire.

Data Disk 1 Backup Disk 1 Data Disk 2 Backup Disk 2 ... Data Disk 3 Backup Disk 3

RAID Levels 2 & 3

RAID levels 2 & 3 use bit-interleaved error-correction schemes. This means that the redundant information required to correct errors is calculated on a bit-wise basis from corresponding bits across the several disks. This means that all heads must always move in lock-step.

RAID Level 2 uses an ECC similar to that used in many silicon-based memories. Often times, a Hamming code is used -- this requires Log (N) disks be used for error correction.

RAID level 3 uses a simple parity bit. Although simple parity can not in general be used as an error correcting code, just as an error detection code, this isn't the case with disks. Most often we can determine which disk has failed. Provided no other errors occur, the parity bits can be used to determine the value of each bit on the failed disk. The good news is that only one parity disk is required, and this expense is amortized over all data disks.

RAID level 2 is rarely implemented because of the number of disks required for redundancy. ECCs are unnecessary given the reasonably high level of reliability of most disks.

Although RAID level 3 doesn't suffer this difficulty, it is also rarely implemented. Since all of the heads must move in lock-step, this type of array can't really support concurrency.

RAID Level 4

Unlike RAID levels 2 & 3, RAID Level 4 is designed to allow concurrent accesses to the disks within the array. it maintains the small wastage of RAID level 3.

This is achived by using block-interleaved parity. One disk contains only parity blocks. Each parity block contains the parity information for corresponding blocks on the other disks. Each time a write is performed, the corresponding parity block is updated based on the old parity, the old data, and the new data.

The parity bit is the XOR of corresponding bits across all disks. Consider the example below:

Since the parity disk must be accessed every time a write is performed to any other disk, it becomes a hot spot.

Disk 0 Disk 1 Disk 2 Parity Disk
D0,0 D0,1 D0,2 P0
D1,0 D1,1 D1,2 P1
D2,0 D2,1 D2,2 P2
D3,0 D3,1 D3,2 P3

P0 = D0,0 XOR D0,1 XOR D0,2

Although it might initially seem that every disk must be accessed each time any disk is written, this is not the case. Given the old parity, the old data value, and the new data value, we can compute the new parity without reading any other disk.

Consider a write to D0,2, the new parity can be computed as follows:

P0-new = (D0,2-old XOR D0,2-new) XOR P0-old

Normal read operations require access only to one disk. Normal write operations require access to the target disk and to the parity disk.

Once any data disk fails, read and write operations require access to all disks. The corresponding parity bit and data bits are XOR'd to calculate the missing data bit.

RAID Level 5

RAID level 5 operates exaclty as does RAID level 4, expect that the parity block are distributed among the disks. This distributs the parity update traffic among the disks, alleviating the hot spot of the single parity disk. Typically the parity blocks are placed round-robin in a rotated fashion on the disks. This is known as rotated parity

Disk 0 Disk 1 Disk 2 Disk 3
D0,0 D0,1 D0,2 P0
D1,0 D1,1 P1 D1,3
D2,0 P2 D2,2 D2,3
P3 D3,1 D3,2 D3,3

P0 = D0,0 XOR D0,1 XOR D0,1

P3 = D3,1 XOR D3,2 XOR D3,3

Normal read operations require access only to one disk. Normal write operations require access to the target disk and to the disk hold the parity for that data block.

Once any data disk fails, read and write operations require access to all disks. The corresponding parity bit and other data bits are XOR'd to calculate the missing data bit.

RAID 6

RAID 6 is essentially identical to RAID 5, except that it incorporates two different parity blocks. This enables it to function through not only one, but two, disk failures -- for example a disk failure during the replacement and reconstruction from a prior disk failure.

As disks become larger and recovery times increase, the window of vulnerability for a second failure also increases. RAID 6 guards against this and is increasingly being seen as essential in high-reliability systems.

Hamming Distance and RAID Levels 3-6?

If we need a Hamming distance of (2D + 1) to detect a bit bit error, how can we get away with only one parity disk -- don't we need Log 2 N, as above?

Actually no. The big difference between disks and memory or a network is that we can usually know which disk has failed. Disk failures are usually catrastrophic and not transient. If we know which disk has failed, which is usually easy to figure out, we can correct a 1-bit error, given simple parity. We just set that bit to whatever it needs to be for the parity bit to be correct.