Return to the lecture notes index
February 28, 2008 (Lecture 13)
Agreement In Light of Failure Isn't Easy: Two Classic Problems
This semester we've spent a good bit of time discussing the construction
of fault-tolerant systems and the robustness of algorithms in light of
failure. But we've never really stopped and taken a good look at the nature
of failures themselves.
Today we'll discuss two classic problems, the Two Armies Problem
and the Byzantine Generals Problem. These problems illustrate
communications failures and processor failures, respectively.
The Two Army Problem
Consider two waring armies, the Red Army, and the Blue Army. The Blue
Blue Army is camping in a mountain valley. The Red Army, while larger
and more powerful, is divided into two groups hiding in the surrounding
mountains.
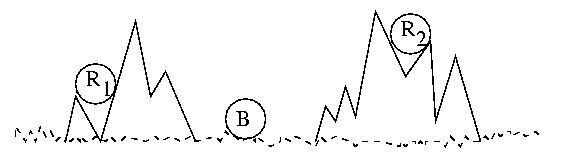
If the two Red Army platoons attack the Blue Army together and at
exactly the right time, they will prevail. The longer they wait, the more
surpised the Blue Army will be by the attack. But if they wait too long,
they will run out of supplies, grow weak, and starve. The timing is
critical. But if they are not coordinated, they will surely lose.
They must attack at exactly the same time.
When the time is right R1 will send a messenger to
R2 that says, "Attack at dawn!" But R1 may
become concerned that R2 did not get the message and
consequently not attack. If that happens, R1 will
be defeated. Alternately, R2 may become concerned that
R1 will beocme concerned, so they may not attack, leaving
R1 to be defeated in solitude.
So what if they agree that the recipient of the message, R2,
will return an ACK to the sender, R1? This is just one level
of indirection. The R2 may become concerned that the ACK was
lost and not attack. Or R1 may become concerned that
R2 became concerned and did not attack. This problem can't be
solved by ACK-ACK, or even ACK-ACK-ACK-ACK -- more ACKs just add more
levels of indirection, but the same problem remains.
Another issue might be fake messages. What if the Blue Army sent an
imposter to deliver a message to R2 telling them to attack
too early. They would be defeated if they followed it. But if they
did not obey messages for fear that they were fraudulant, R1
would be defeated when they did attack, even after advising R2.
This fear might also prompt an army from acting upon a perfectly valid
message.
The moral of this story is that there is no solution to this probem if the
communications medium is unreliable. Please note that I said
medium, not protocol. This is an important distinction.
A reliable protocol above an unreliable medium can guarantee that a
message will eventually be sent, provided of course that the
recipient eventually becomes ready and accessible. But no protocol
can guarantee that a message will be delivered within a finite
amount of time -- error conditions may persist for long and
indeterminate amounts of time.
The Byzantine Generals Problem
One day, many moons ago, the Turkish Sultan led an army to invade the
Byzantine Empire, Byzantium. The Emperor had several smaller armies to
defend the Empire. The leaders of these individual armies needed to be
carefully coordinated in order to defend the city against the Turks.
They needed to receive frequent updates about the strength of the other
armies in order to act properly.
They were aware of the communications problems that led to the defeat of
the Red Army, so they used careful encryption and error correction to
exchange messages. But they had a new problem -- traitors. The Byzantines
suspected that one of their generals was a traitor who would lie about
the strength of his army in order to undermine their defense.
In order to combat this problem and detect the traitor, they established
a protocol for exchanging messages:
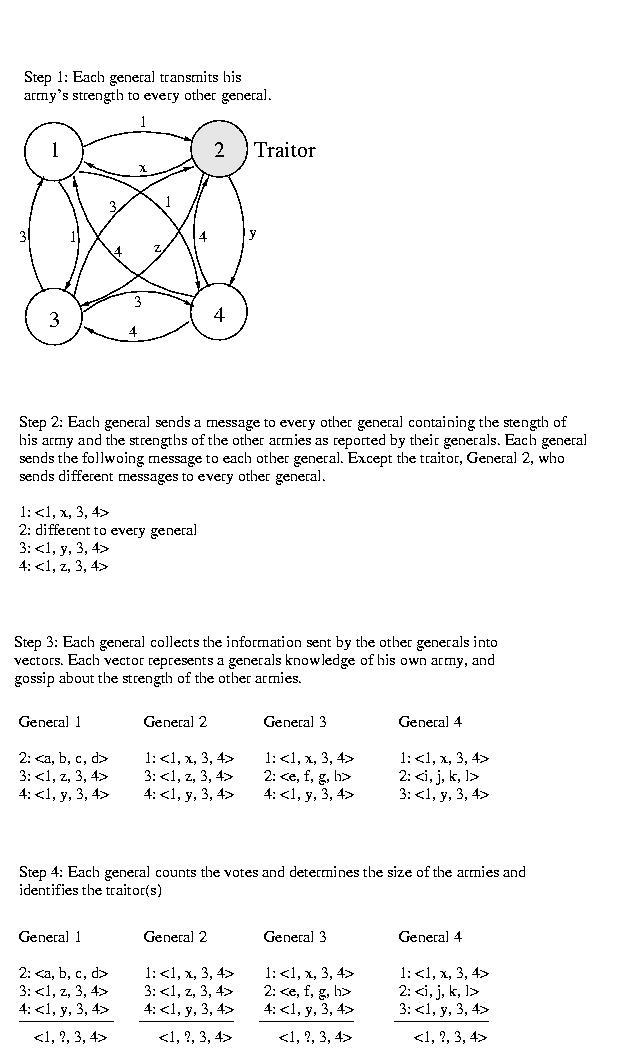
- Each general should transmit the strength of his army to
every other general using a reliable messenger.
- Once each general has collected this information, he should send
it to every other general. Once this happens, each general
knows what every other general thinks about the strength of each
army.
- Each general should then determine the strength of each army by
considering each general's report of that army's strength as a
vote in favor of an army size. If a majority of the generals
agree about the size of a particular army, that size should be
believed. Otherwise, the size of the army should be considered
unknown and the general of the unknown sized army should be
suspected of treachery.
Note:
It is important that only the reports from the other
generals as part of step 2 be counted. It duplicates information
if the information from step 1 is counted.
Example
How Many Traitors can the Byzantines Tolerate?
It is a theoretical finding that if there are T traitors, there must
be (2T + 1) loyal generals for the loyal generals to determine the
sizes of the loyal armies and to identify the traitors.
We won't provie this property in this class. The intuition behind it is
this. Normally, we'd expect to find that we need (T+1) loyal generals
to outvote the T traitors. But, upon a more careful look, this isn't
actually correct. Take a careful look at the vectors. Notice that, for
each disloyal general, we've got two different types of corruption -- the
entire vector provided by that general as well as that general's entry in
each and every other vector.
As a result, we need to outvote both these T broken vectors -- and the
T broken entries within the other vectors: (2T + 1).

Does This Always Work?
Well, of course not. This wouldn't be Distributed Systems if we actually
gave you a comprehensive solution to a problem -- these are hard problems,
afterall.
If the disloyal general tells the same lie to all of the generals, they
will each agree to the wrong value. For this reason, based on this
pedagogical story, undetectible errors (faulty hardware, not faulty
communications) are known as Byzantine Errors by computer scientists.
So, what would it take?
If each general is forced to sign his message, and all messages are repeated
to all generals -- including the signatures, this problem can be solved
-- only one loyal general is required. (If they are all disloyal, who is
checking, anyway?) In that case, it would be known which general had
signed the inconsistent messages -- solving for the consistent lie would
still require a scouting mission. (Additionally, it is required that the
authenticity of the signatures can be readily verified, as can forgery).
What is a digital signature? Think back to prior courses and discussions
about PGP, and other public-private key algorithms. A signature is
the private key that si used to encrypt the message. The sender is
authenticated if the right private key decrypts the message.
What's the Moral of the Story?
Failures can be expensive to detect -- sometimes impossible. This means
that distributed agreement may not be expensive -- or impossible. Sometimes
we have to pay the price, sometimes we don't. The successful design and
implementation of distributed systems depending on knowing what we can
do, what we can do, and what we should do.
References
Today's discussion, and the Two Army Problem, in particular,
follow that of Tanenbaum very closely. When I first prepared
this lecture, the citation was as follows:
Tanenbaum, A.,Distributed Operating Systems, Prentic Hall, 1990,
219-222.
In his present edition, this discussion is captured in the following:
Tanenbaum and van Steen, Distributed Systems: Principles and
Paradigms, Prentice Hall, 2002, 371-375.


