Stacks
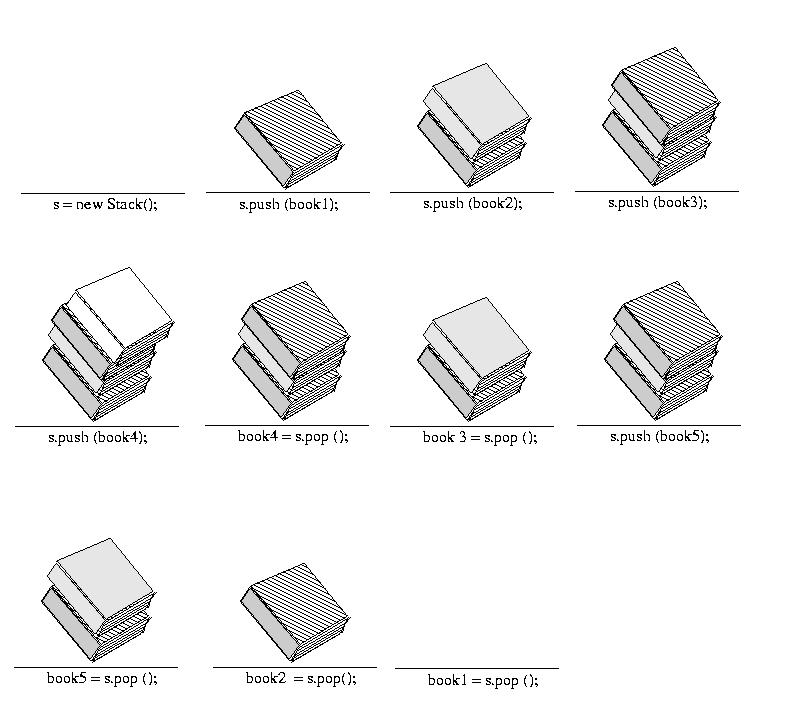
In the real world, a stack is a way of organizing something where all of the items are piled on top of one another. We might have a stack of papers on a desk, a stack of books, etc. The easiest way to work with the items that are in the stack is to take off the one on the top and process it. The easiest way to add something to the stack is to put it on the top of the pile.
In computer science, we can implement a stack in a similar way. A stack is a first-in-last-out data structure where we always remove the item which has most recently been added to the stack. This means that in order to remove the first item that we added we first have to remove everything else, which is why we say that it is a first-in-last-out structure.
Let's look at the operations on a stack:
Consider the example of a "book stack" shown below:

Why Use Stacks?
Much as was the case for queues, stacks are far less powerful than linked lists or vectors. We don't use them because we want more power -- we use them because we want more discipline. We'll talk about many examples of their use, beginning next class.But for now, let me mention some things that might, or might not, be familiar to you. If not, don't fret -- we'll get there. Sometimes we use stacks to store the intermediate steps in a calculation. Consider, for example, RPN calculators, like the famous HP scientific calculators.
Or, if you remember discussing the "call chain", a.k.a, the "call stack" in your intro class, you might now realize that we can model the calling and returning of methods using stacks. Each time we call a method, we push() it onto the stack. And, each time a method returns, we can pop() if off of the stack. Then, at any time, this stack will model the state of execution of our system.
Or, perhaps most familiar at all is the "undo stack" used by popular software to allow you to undo actions. Each time you make a change, it pushes it onto the stack. That way, you can choose to "undo", which will pop the stack to figure out what you did and then undo it. By using a stack, instead of a random-access or sequentially accessed collection of changes, we ensure that the user is offered a choice of prior versions of the document, in an understandable one-at-a-time way. Without this, the "undo" option would really degenerate into an unorganized menu of the opposites of popular options, right? Think about it -- here are the opposites of a bunch of things you did recently, would you care to select one? That would be an odd feature, indeed!
Implementing A Stack With A Linked-List
Before we can implement a stack with a linked-list, we need to decide which end of the list we want to use as the top of the stack. Do we want to add and remove elements from the head, or do we want to add and remove elements from the tail?Adding to the head only requires us to rearrange a few references in order to include the new node in the list, as does adding to the tail. Removing from the head only requires us to rearrange a few references in order to remove the first node from the list. Removing from the tail is a little more complicated because we have to set the second-to-last element to be the new tail. Since we cannot go backwards in a singly-linked list, we have to start at the beginning of the list and traverse until we reach the second-to-last node. In a long list, this is time consuming, so we will use the head of the list as the top of the stack.
The following code implements a stack using a linked-list:
/* * This class implements a stack using a linked-list. It has the standard * stack behaviors push and pop, as well as a peek method to see the item * on the top of the stack without removing it, and an isEmpty method to * see test if the stack is empty. */ class ListStack { private LinkedList stack; // stores the items of the stack /* * Constructor. It initializes a new LinkedList to be used for the stack */ public ListStack() { stack = new LinkedList(); } /* * This method adds a new item to the top of the stack */ public void push(Object addObj) { // we are using the head of the linked-list as the top of the // stack, so we add to the head stack.addHead(addObj); } /* * This method remove the item from the top of the stack */ public Object pop() { // we are using the head of the linked-list as the top of the // stack, so we remove from the head return stack.removeHead(); } /* * This method returns the item at the top of the stack without * removing it */ public Object peek() { // set the index of the linked-list to be at the head stack.resetIndex(); // return back the item stored at the head return stack.getIndexedNode(); } /* * This method tests whether or not the stack is currently empty * * if there is nothing at the head, then there is nothing in * the stack */ public boolean isEmpty() { // set the index of the linked-list to be at the head stack.resetIndex(); // return true if the head of the list is null, false otherwise return (null == stack.getIndexedNode()); } }
To help you to gain a clear understanding of how stacks work, we'll apply stacks to the pursuit of evaluating arithmetic expressions.
I'm sure that the following expression looks familiar to you.
2 + 2
The style used to write this expression (two, then plus, then two) is called infix notation, and it's the style most commonly seen in arithmetic. But there are other ways of writing arithmetic expressions.
You probably know that the 2's are operands, and that the + is the operator associated with the operands. The plus operates on the 2's. Infix notation order is "operand operator operand" for all binary operators (e.g., + - * /).
But have you ever seen the same expression written this way?
2 2 +
maybe on a calculator display?
This is called postfix notation, because the operator comes after its operands.
When expressions get more complicated, parentheses come into play. For instance, take the expression
(3 + 6) * (2 - 4) + 7.
Remember the order of operations that you learned as a child in arithmetic?
Postfix notation, on the other hand, looks like this:
2 4 +.
Now, instead of having "operand operator operand", you have "operand operand operator".
The "post" in postfix means that the operator comes after its operand(s).
Look at the infix expression.
(4 + 5) * 3 - 7
A quick infix evaluation will lead you to a result of 20.
In postfix notation, this expression would be
4 5 + 3 * 7 -
You know how to evaluate an infix expression, probably in your sleep. But do you know how to evaluate that same expression if it's in postfix notation? Here's how.
Work through the postfix expression from left to
right. Every time you encounter an operator, evaluate the two operands
that came before it. Save the result of the operation on the two
operands, and continue until you have evaluated the
entire expression.
What's so great about postfix notation? As you can see, it eliminates
all parentheses. Postfix notation is used in some applications
because it saves on memory. After a few times of looking at
postfix notation, it becomes easier to read.
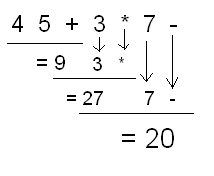
So how do you convert an infix expression to a postfix expression?
Converting an expression from infix to postfix is easy.
The first thing you need to do is fully parenthesize the expression.
So, the expression
(3 + 6) * (2 - 4) + 7
becomes
(((3 + 6) * (2 - 4)) + 7).
Now, move each of the operators immediately to the right of their
respective right parentheses.
If you do this, you will see that
(((3 + 6) * (2 - 4)) + 7)
becomes
3 6 + 2 4 - * 7 +
Converting from Infix Notation to Postfix Notation by Hand
Take a close look at the arrowheads. To convert an infix expression to postfix, you simply place each operator in the infix expression immediately to the right of its respective right parenthesis. Then you rewrite the expression in the new order, and what you get is the same expression in prefix notation.
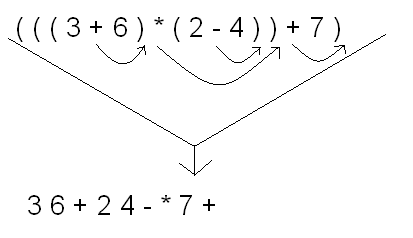
Try converting some infix expressions of your own into prefix notation. As you can see, it's easy to do.
Read in one symbol at a time from the postfix expression.
When you're done with the entire expression, the only thing left on the stack should be the final result. If there are zero or more than 1 operands left on the stack, either your program is flawed, or the expression was invalid.
Very Important:
The first element you pop off of the stack in an operation should
be evaluated on the right-hand
side of the operator. For multiplication and addition, order doesn't
matter, but for subtraction and
division, your answer will be incorrect if you switch your
operands around.
Step through this example. By the end of it, it will be clear to you how a stack can easily evaluate a postfix expression. Here, we use a stack to evaluate the expression 4 5 + 9 * 3 + 3 /.

Recursive Thinking
When we were first learning to program, we handled repetative tasks with equally repetitive programming -- the same pieces of the program were repeated, perhaps with only slight modification, as many times as necessary to complete the entire job.Later we learned to write more generic code and to use loops to apply it as many times as necessary, perhaps, through parametrization, to different parts of the problem. This approach is called iterative programming.
Today we are going to discuss another, very powerful way of viewing some problems -- recursion. With recursion, a method divides its task among itself -- it calls itself.
A Bit of "Under the Hood"
The compiler makes use of the stack data structure to keep track of method invocation. Think about it: Each time a method is called, execution jumps to a completely different part of the program, and entirely new variables exist. These variables might have the same names as other variables in the program, but they are not the same -- they can have different values. And, once the method returns, these local variables "go away" and execution picks right up where it left off. Additionally, parameters need to be communicated to the method when it called, and a return value needs to be communicated to the caller, upon return.The compiler does this using a stack, often called the runtime stack. When a function is called, the compiler pushes the parameters onto the stack, followed by the return address. It then pushes empty space (allocates space) on the stack for all of the local variables. This state, which is stored on the runtime stack, and is assocaited with a single activation of a method, is known as a stack frame.
When the method returns, the compiler pops its stack from from the stack, revealing the return address, and stores the return value on the stack. Upon return, the caller then pops the return value from the stack.
Additionally, there is plenty of other state information associated with the activation for each function that is stored within the stack frame. For example, if there are only a few parameters, they are often passed in registers, fast memory within the CPU. These registers need to be saved to and restored from the stack when a method is called and upon its return. There are also some pieces of metadata about the stack, itself, such as pointers to the beginning of each stack frame, &c.
For this class, we're not going to get bogged down in the details -- those are covered in 15-213. But, it is critical that you realize that each instance of a function has its own parameters and local variables. It is also critical that you realize that the compiler uses a stack to manage function invocation.
For our purposes, when I draw the runtime stack, I am only going to draw these the things that are critical to us -- the paramters, the local variables, and the return value. And, although the stack is used to communicate the return to the caller, I'm going to, most often, draw in on an arrow connecting one stack from to the next. On the whiteboard, this is just a really clear way of showing that a method returns, popping the stack, and returning a value.
The 2n Example
If asked to computer 2n might be to think about the problem this way: "Start out with one and multiply it by two n times." This is an iterative approach and can be implemented by initializing a value to 1 and multiplying it by 2 n times:
public static int pow2 (int n) { int answer=1; for (int index=0; index < n; index++) answer *=2; return answer; }Another perspective might be this "Multiply 2n-1 by 2. If you don't know 2n-1, figure it out by multiplying 2(n-1)-1 by 2. Nest this logic as deeply as necessary, until you reach -- for example, we know that 20 is 1.
static int pow2_rec (int n) { if (0 == n) { // This is the base case -- 20 is 1 // So if we are asked for 20, we return 1. return 1; } else // If we don't know the answer, we use recursive logic to figure // it out by multiplying 2n-1 by 2. return (2*pow2_rec(n-1)); }
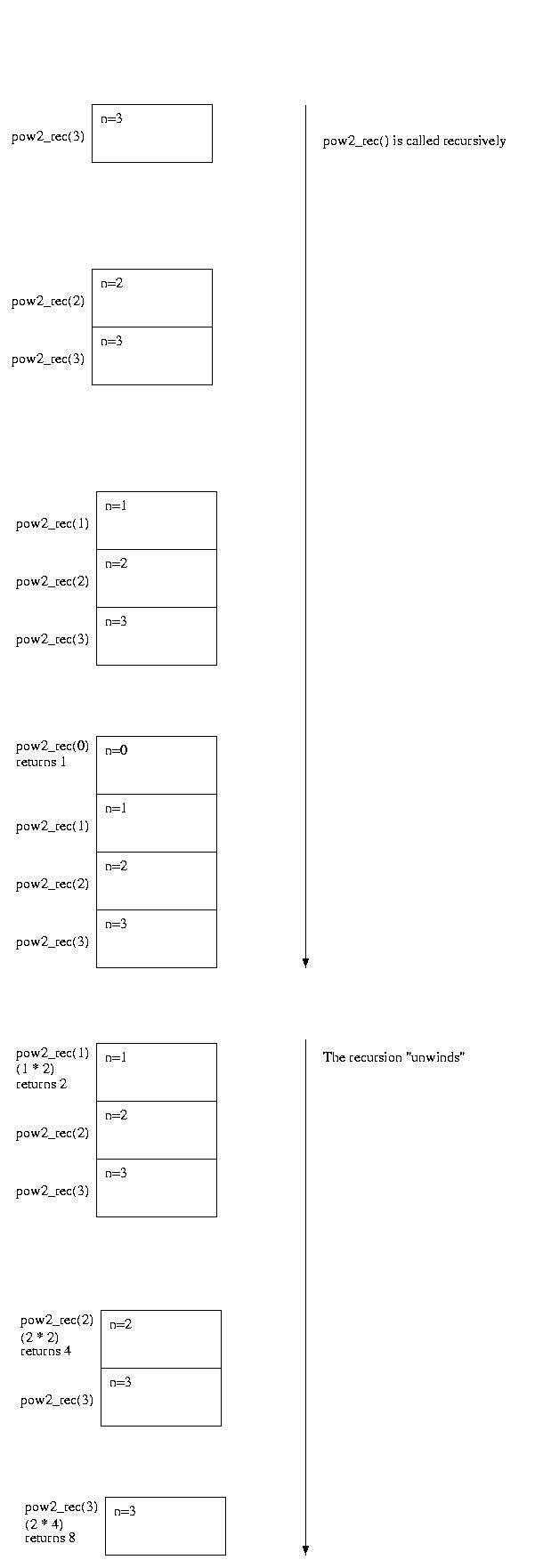
A Trace of pow2_rec(4)
Let's take a look at the execution of pow2_rec(4).
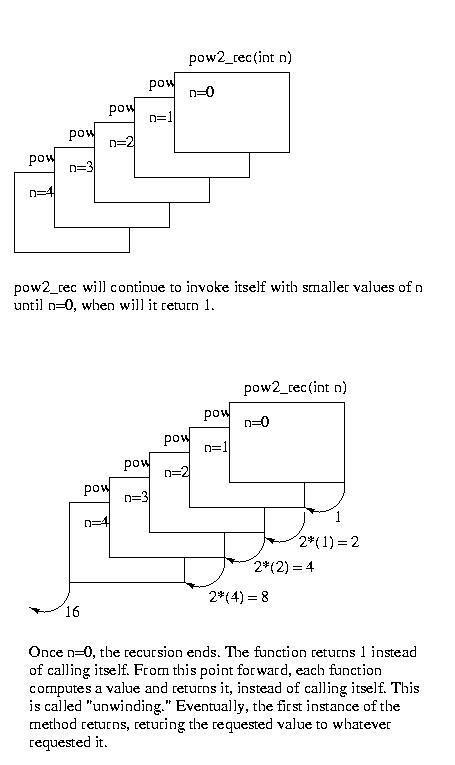
Methods are invoked using a stack. Each time a method is invoked, the state of the method making the call is pushed into the stack. When a method returns, the state is popped off of the stack and restored. It is important to realize that each instance of a method has its own local variables -- they are actually part of its stack frame.
The following diagram shows the changes in the stack as pow2_rec(3) is evaluated. In the recursive phase, the stack grows as new frames are created for each invokation of the method. In the "unwinding phase" the stack frames are popped off as the methods return values to the caller.
The n! (Factorial) Example
As another example, recursion can be used to calcualte the factorial of a number. Remember that the factorial of a number is defined as follows:0! = 1
N! = N * (N - 1)!, N > 0
public static int fact_rec (int n) { if (0==n) return 1; else return (n * fact_rec(n-1)); }Notice that like the pow2_rec() method, fact_rec() has a non-recursive case that is guaranteed to occur and will terminate the recursion, allowing it to unwind. If there is no non-recursive case, or if there is not guarantee that the non-recursive case will ever occur, infinite recursion might result. Infinite recursion is much like an endless loop -- the program will run forever (or terminate, because there isn't enough memory left for the stack).
The printReverse Example
Recursion isn't just useful for mathematical things. It might also make LIFO (last in first out) operation easier, because of the stack that is created by the recursive function calls. This example takes advantage of this property of recursion to print a string in reverse.
public static void printReverse (String s) { if(s.length() >0) printReverse(s.substring(1, s.length()-1); else return; System.out.println(s.charAt(0)); }This method calls itself with a smaller and smaller string, until it has an empty string. Once it has an empty string, it starts to unwind. As it unwinds, it prints the first character in the substring. Since recursion is based on a stack, it returns in LIFO order. The string is printed in reverse.
Fibonacci Numbers
The Fibonacci sequence is defined as follows:Fib0 = 1
Fib1 = 1
Fibn = Fibn-1 + Fibn-2, n > 1
We can computer the nth number in the Fibonacci sequence readily using recursion:
public static void fib (int n) { if (n==0) return 1; if (n==1) return 1; return (fib(n-1) + fib(n-2)); }But while this code is very simple, makes sense, and is easy to prove correct, it does have a problem. It is very slow and can't compute large Fibonacci numbers. The problem is that it takes a long time to copy data onto the stack....and the stack will grow very large. Each call to Fib() generates two other calls -- the size of the stack doubles at each level! This is called the binomial expansion.
This code can be rewritten nonrecursively to eliminate this limitation and run faster -- but the price is readability:
public static int fib (int n) { if((n==0) || (n==1)) return 1; int prevPrev = 1; int prev = 1; int sum = 0; for(;n>1;n--){ sum += prev +prevPrev; prevPrev = prev; prev = sum; } return sum; }We should never have to use recursion. We should never solve large problems using recursion. There is only the way that we should use recursion is if there is something on the stack that we need to save.