15-112 Lecture 12 (July 17, 2014)
Recursive Thinking Without Recursion: Maintain a Stack
It is important tho realize that, although recursive thinking is a
powerful tool for working through many types of problems, and many
languages support recursive function calls -- recursive thinking can be
implemented without recursive code. Anything that can be implemented
with recursive code can be implemented without.
Consider, for example, pow2():
def pow2(n):
if (n == 0): return 1
return 2*pow2(n-1)
How can we implement this without making a recursive function call? Recall
the mechanics behind recursion. It pushes a stack frame onto the
stack each time a function is called, expands it as needed with local
variables, and pops it off the stack upon return.
Given this, there is no reason we can't do the same. We can "simply" maintain
our own stack. For example, we can create a list and "push" things
onto it by appending and "pop" things from it by removing the last item.
The restult is the implementation of recursive problem solving without
recursion.
#!/usr/bin/python
def pow2(n):
stack = []
while (n != 0):
stack.append(n)
n=n-1
result = 1
while (len(stack) > 0):
result *= 2
stack.pop() # Same as, pop(len(stack)-1)
return result
print pow2(4)
Recursive Thinking Without Recursion: Tail Recursion
Certain forms of recursion are said to be tail recursive. In these
cases, the values on the stack are not consulted during the unwinding phase,
so the stack isn't actually needed for this purpose.
If we take our pow2(n) function as an exmaple, it is almost tail recurive --
but not quite. It multiplies the value on the stack by 2 during the unwind.
So, let's fix that. The version below does the computation first and saves it,
so the recursive call is "cleanly" last.
def pow2(n, pow_so_far=1):
if n == 0:
return pow_so_far
else:
return pow2(n - 1, 2 * pow_so_far)
Given the formulation above, we see the stack isn't necessary and can
rewrite the above using a while loop:
def pow2(n, pow_so_far=1):
while (n != 0):
pow_so_far = 2 * pow_so_far
n = n -1
return pow_so_far
Notice how, in the above example, what ww ddi can be done systematically in
all cases of tail recursion: we replaced the recursion with a while loop,
stopped at the base case, perfomed the update in the body, and returned
at the end.
Some languages require or allow the automatic replacement of tail recurison
with a while loop -- it is a form of optimization. This is done to improve
the speed of the code. Python doesn't do this. If you happen to be interested,the reasons have been very well discussed here and here.
To Recurse or Not To Recurse?
Don't worry about tail recursion. Don't even worry about the cost of
recursion. Don't worry about eliminating recursion. There is plenty of time
for that later. Right now, I want you to:
- Express yourself clearly in code, recursively or otherwise
- Know that recursion, like anything else, has costs and benefits.
Know that, later on in life, when you start addressing larger
problems, you mayh need to compromise expressiveness for
performance. And, when you get there, you may explore ways to
solve certain large problems without recursive implementations
or discover that you don't need to worry about it, because in
certain special cases, your tools can do it for you.
Binary Recursion and a Recursion Tree
Quickly recall fib(n) from last class:
#!/usr/bin/python
def fib(n):
if (n == 0):
return 0
if (n == 1):
return 1
return fib(n-2) + fib(n-1)
It was the first example we'd seen of binary recursion, which is the
case where a single recursive call can directly make two more recursive
calls. Binary recursion is interesting, becuase it can "blow up", doing a
lot of work really quickly. As the n increases incrementally
(linearly), the tree doubles in size, resulting in rapid(exponential)
growth in the amount of work needed.
For example, consider the call tree for fib(4), shown below:
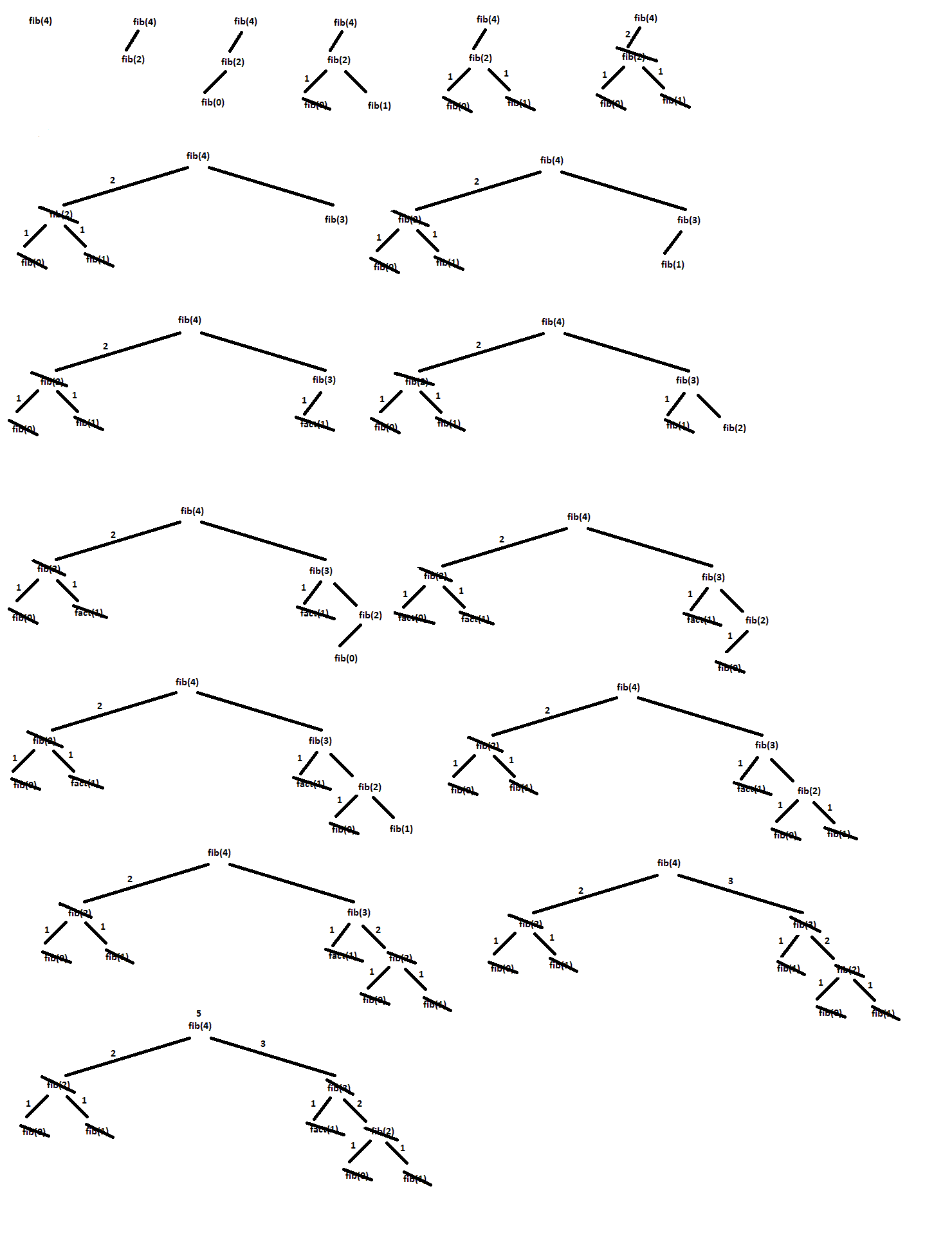
Memoization: A Better Way?
What is interesting about the tree above is that it not only grows
rapidly -- but it is very redundant. It computes fib(0) twice,
fib(1) 3 times, and fib(2) twice.
One way to save time is to store the vales the first time we
calculate them, so we can used the stored values rather than
recomputing for subsequent uses. This technique is called
memoization. You'll talk a lot about it in 15-210.
But, we worked through a couple of implementations for this
example in class.
The first example is somewhat straight-forward. We use a list
to store values as we compute them. We pre-popualte it with
our base cases of 0 and 1. As we need values, we try to look
them up. If they aren't there, we get an exception, add them,
and keep chugging along:
`
#!/usr/bin/python
fibs = [1,1]
def fib(n):
try:
return fibs[n]
except:
fibs.append((fib(n-2) + fib(n-1)))
return fibs[n]
print fib(0)
print fib(1)
print fib(2)
print fib(3)
print fib(4)
print fib(5)
print fib(6)
`
One interesting observation is that we learn about the series from
lowest-to-highest, from left-to-right in our list. So, instead of
using exceptions, we can also just look at the length of the list
as in the example below:
`
#!/usr/bin/python
fibs = [1,1]
def fib(n):
if (n >= len(fibs)):
fibs.append((fib(n-2) + fib(n-1)))
return fibs[n]
print fib(0)
print fib(1)
print fib(2)
print fib(3)
print fib(4)
print fib(5)
print fib(6)
`
The cool thing about this approach is that as n grows "linearly",
e.g., from 1, to 2, to 3, to 4, to 5, to 6, to 7, etc, so does the amount
of work. For example, each time n gets one bigger -- we only need
to add one more thing to the list. Before, each increment of n
resulted in approximately a doubing of the size of the recursion tree, which
illustrates the doubling of the amount of work and time required.
Cool, huh? You'll learn a ton more about this in 15-210. This was just a
preview.
