We then drove down and took a deeper look at fib(), as implemented below:
#!/usr/bin/python
def fib(n):
if (n == 0):
return 0
if (n == 1):
return 1
return fib(n-2) + fib(n-1)
It was the first example we'd seen of binary recursion, which is the
case where a single recursive call can directly make two more recursive
calls. Binary recursion is interesting, becuase it can "blow up", doing a
lot of work really quickly. As the n increases incrementally
(linearly), the tree double sin size, resulting in rapid(exponential)
growth in the amount of work needed.
For example, consider the call tree for fib(4), shown below:
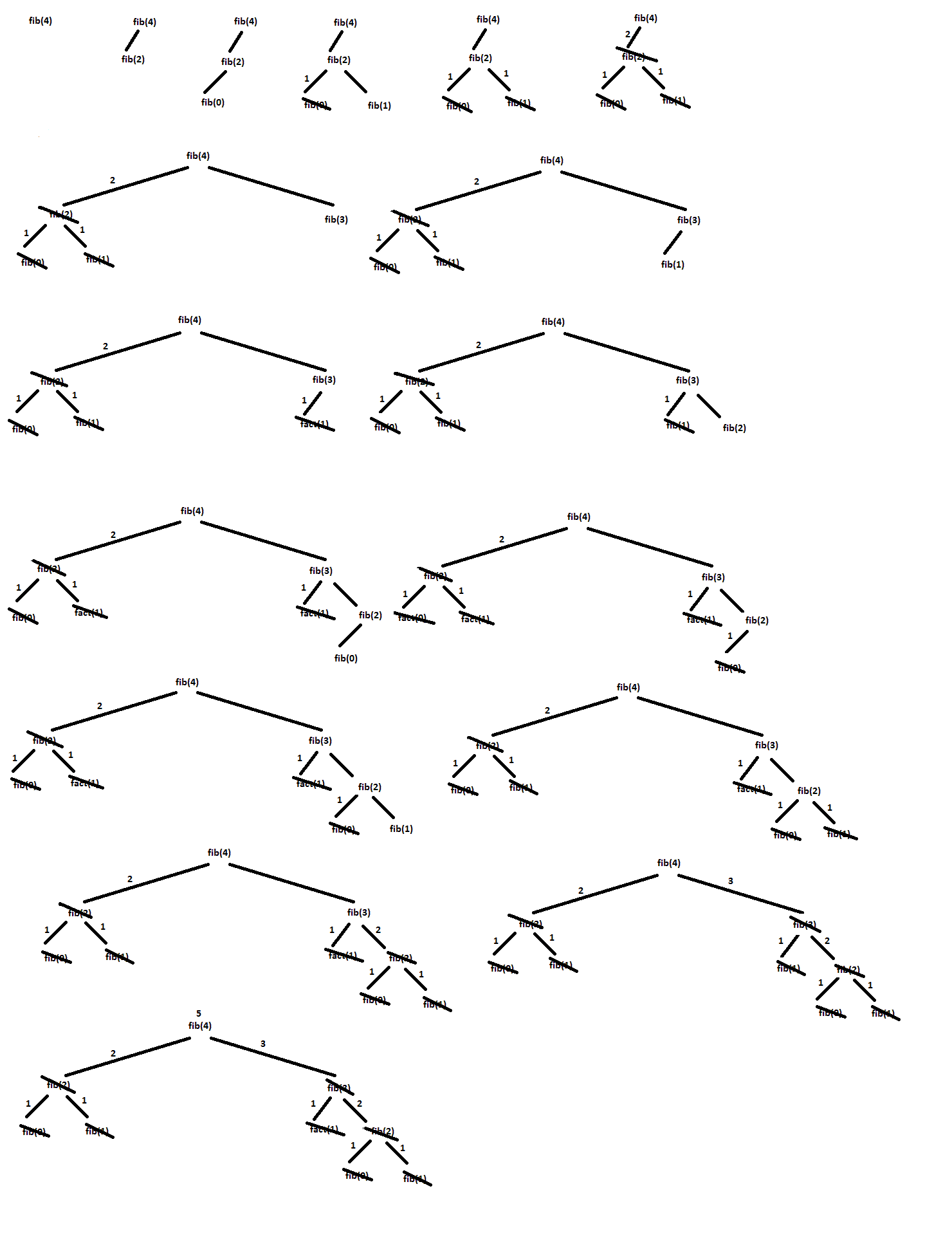
What is interesting about the tree above is that it not only grows
rapidly -- but it is very redundant. It computes fib(0) twice,
fib(1) 3 times, and fib(2) twice.
One way to save time is to store the vales the first time we
calculate them, so we can used the stored values rather than
recomputing for subsequent uses. This technique is called
memoization. You'll talk a lot about it in 15-210.
But, we worked through a couple of implementations for this
example in class.
The first example is somewhat straight-forward. We use a list
to store values as we compute them. We pre-popualte it with
our base cases of 0 and 1. As we need values, we try to look
them up. If they aren't there, we get an exception, add them,
and keep chugging along:
fib-memo1.py:
`
#!/usr/bin/python
fibs = [1,1]
def fib(n):
try:
return fibs[n]
except:
fibs.append((fib(n-2) + fib(n-1)))
return fibs[n]
print fib(0)
print fib(1)
print fib(2)
print fib(3)
print fib(4)
print fib(5)
print fib(6)
`
One interesting observation is that we learn about the series from
lowest-to-highest, from left-to-right in our list. So, instead of
using exceptions, we can also just look at the length of the list
as in the example below:
fib-memo2.py:
`
#!/usr/bin/python
fibs = [1,1]
def fib(n):
if (n >= len(fibs)):
fibs.append((fib(n-2) + fib(n-1)))
return fibs[n]
print fib(0)
print fib(1)
print fib(2)
print fib(3)
print fib(4)
print fib(5)
print fib(6)
`
The cool thing about this approach is that as n grows "linearly",
e.g., from 1, to 2, to 3, to 4, to 5, to 6, to 7, etc, so does the amount
of work. For example, each time n gets one bigger -- we only need
to add one more thing to the list. Before, each increment of n
resulted in approximately a doubing of the size of the recursion tree, which
illustrates the doubling of the amount of work and time required.
Cool, huh?
