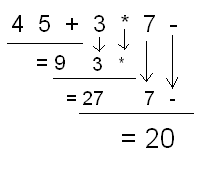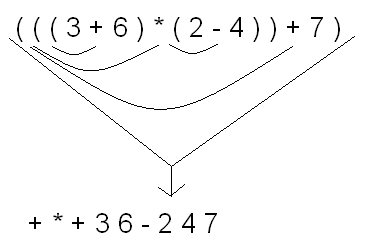Return to the Lecture Notes Index
15-111 Lecture 9 (Friday, May 28, 2004)
Using Stacks for Computation
Before we leave stacks and move on, let's discuss a few more examples
of how stacks can be used to solve problems. Recursion was an example
of how the compiler makes use of a stack to support method invocations
and how we, as programmers, can indirectly exploit that.
This next collection of examples illustrates how we, as programmers, can
make explicit use of stacks to solve problems. These examples like in
the domain of mathematics -- which, I know, can be boring for some. But,
I think they are excellent examples of the power of stacks to solve
problems -- so, even if you aren't interested in thinks with numbers and
funny symbols, please bear with me.
Postfix Notation
Often times, how we represent a problem can make a huge difference in
how readily it is solved. In real estate, it is often said that the
three most important things about a property are location, location, and
location. In computer science, the three most important things needed
to solve a problem are often said to be representation, representation,
and representation.
In representing simple arithmetic expressions, we, as people, often
use what is known as infix notation. This is nothing more
than a fancy term for the way we write expressions, such as "(4+5)/3".
Computers can evalutate expressions written like this -- but, they can
evaluate them much more efficiently, if they are represented in another
notation known as postfix.
Before getting into what postfix notation means, lets review what most of you
know very well: Infix Notation. In infix notation, expressions such as 2+2
are allowed. In this expression, the 2's are operands, and the + (plus) is
the operator associated with the expression. In short, infix notation is
operand operator operand (for all binary operators, such as + - * /). When
expressions get more complicated, parentheses come into play. For instance,
take the expression (3 + 6) * (2 - 4) + 7. Going by the order of operations
that you learned in fourth grade, you evaluated the 3+6, and the 2-4 first.
After you get 9 and -2, respectively, you multiply those together to get -18.
Finally, by adding 7, you achieve a final result of -11.
Postfix notation, on the other hand, looks like this: 2 4 +. Now, instead of
having operand operator operand, you have operand operand operator. The
POST in POSTfix means that the operators come after both operands.
Lets now take a look at the infix expression (4 + 5) * 3 - 7. A quick infix
evaluation will lead you to a result of 20. Now lets take a look at how to
evaluate it in postfix:
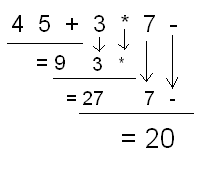
So what's the big deal about postfix notation anyway? Well, as you can see,
it eliminates all parentheses, and after a few times looking at postfix
notation, it becomes easier to read.
Notation Conversions
At first, it may seem like converting from infix notation to postfix notation
might be somewhat of a hassle, but it is in fact very simple. The first thing
you need to do, is fully put parentheses around the expression. So, the
expression (3 + 6) * (2 - 4) + 7 ---> (((3 + 6) * (2 - 4)) + 7).
Now, you move all of the operators just to the right of the right paren.
After performing this, you see that
(((3 + 6) * (2 - 4)) + 7) ---> 3 6 + 2 4 - * 7 +.
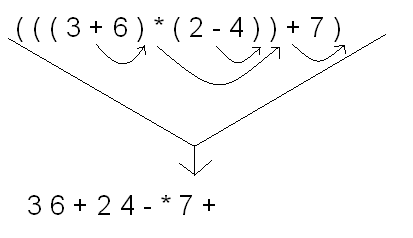
Prefix Notation is just the opposite of postfix, so all
operators will go before both operands. So, to convert to prefix, all you
do is once again fully parenthesize the infix notation, and move all of the
operators to the immediate left of the left paren. . . like so:
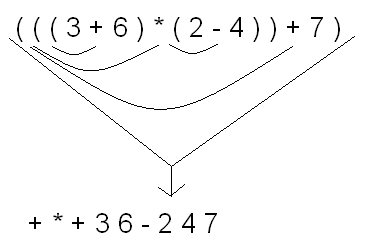
Evaluating Postfix Notation With a Stack
One beautiful thing about postfix notation is that it is easily evaluated
in programming by using a Stack. You read in one symbol at a time from the
expression. Any time you see an operand, you push it onto the stack. Any time
you see an operator, you want to pop two elements off of the Stack, and evaluate
those operands with that operator, and then push that result back onto the
Stack. When you're done with the entire expression, the only thing left on the
Stack should be the final result. If there are 0 or more than 1 operands
left on the Stack, then either your program is flawed, or the expression
was invalid. To help visualize how to implement this, here's yet another
picture.

Notice that the first element you pop off of the stack in an operation will go
on the right. For multiplication and addition, this doesn't make a different.
But for subtraction and division, your answer will usually be way off if you
switch these around.
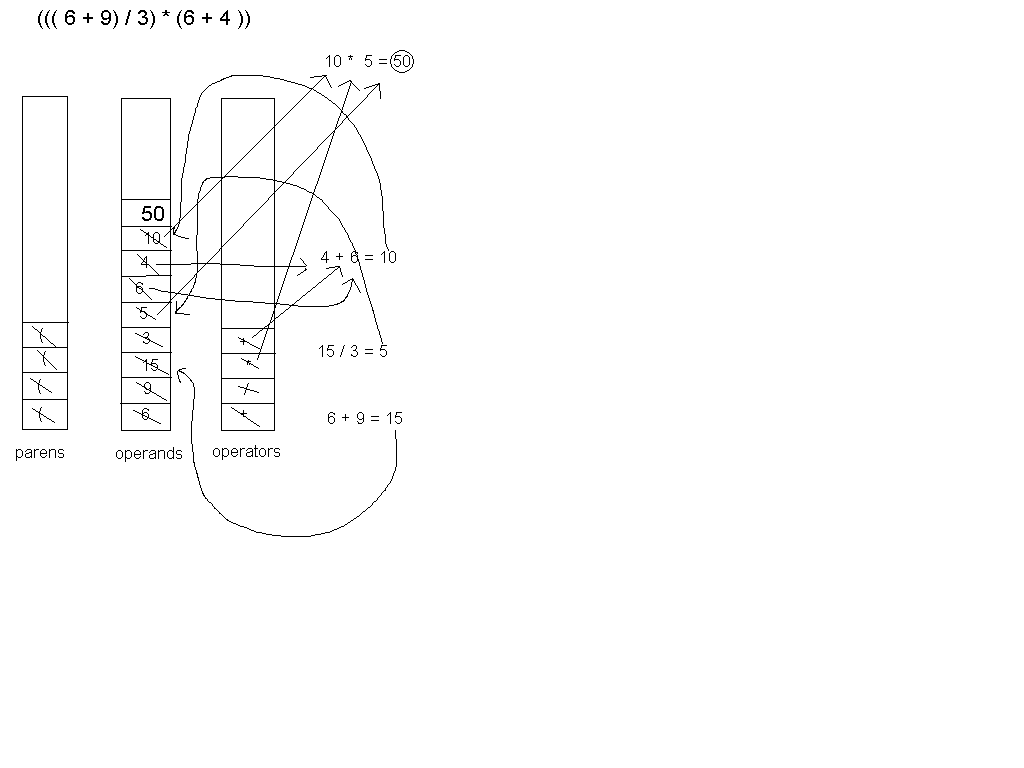
Evaluating a Fully Parenthesized Infix Notation Using Stacks
Evaluating a fully parenthersized infix notation with stacks is substantially
more difficult than evaluating postfix. In effect, we will concurrently convert it to postfix and evaluate the results.
Now, you need 3 stacks: one for the parentheses, one for the operands,
and one for the operators. Just like in the conversions, you need to
fully parenthesize the infix expression before attempting to evaluate it.
To accomplish infix notation, you want to keep pushing elements
onto their respective stacks until you reach a closed parenthesis. As soon
as you see this, pop an operator off the operator stack, and then pop the
appropriate number of operands off the operand stack to perform the operation.
Converting Infix to Postfix
We talked in class today about evaluating fully parenthesized
expressions. I promised to post, for those interested, a discussion
about evaluating incompletely parenthesized infix expressions according
to the order of operations (Please Excuse My Dear Aunt Sally).
Here is the promised discussion. The basic strategy is going to be to
convert the original infix expression into a postfix expression, and
then to evaluate that expression, as we've already discussed.
Here's the big picture:
- It is important to observe that operands never move. They appear
in the same order in infix and postfix expressions. When we
encounter an operand, we will immediately output it.
- Operators will always be pushed onto the stack. This is because
operators always appear later in a post-fix expression than they
do in the infix expression. This is because they appear before the
second operand in infix, but after the second operand in postfix.
- ( are always stacked, since they must be paired with the
corresponding ).
- ) force the popping of the stack, up to and including the
(
- We pop operators from the stack when we they have a higher precedence
than an operator just read from the input.
But this leaves many holes. How do we determine the precedence of an
operator on input?
Well, "Please excuse my dear Aunt Sally."
- ()'s must be the highest
- * and / should be equal, below (), and above + and -
- + and - should be equal, and below * and /
But what if the expression is not fully parenthesized? Then we must
give precedence to the operations on the left. This can be accomplished
by giving operations on the stack a higher precedence than the same
class of operation in the input, without changing its relationship to
operations of a different class.
Parentheses are a special case. Since a ) parenthesis should force the
stack to be popped until the (, it should have a lower precedence than
anything else and it will never be pushed. This may seem paradoxical
given the precedence that we described, but it is the ( that has
the highest precedence on input.
( should have a precedence of 0 to ensure that all of the operators that
can occur within the ()'ed expression can be stacked within it.
Given this, the following precedence table is a simplest solution:
| |
Precedence |
| Operator |
Stack |
Input |
| ) |
N/A |
0 |
| ( |
0 |
5 |
| +,- |
2 |
1 |
| *,/ |
4 |
3 |
The Algorithm
- Step 0: Initialize the stack by pushing a "(" -- this serves
to mark the beginning of the stack and give it an initial
precedence. Append a ")" to the input to pop the initial
"(" from the stack.
- Step 1: If the input is empty, go to Finished.
- Step 2: Read one token (operand, parenthesis, operator) from the
input.
- Step 3: If the token is an operand, output it and goto Step 1.
- Step 4: Look up the precedence of the input token in the "Input"
column of the precedence table.
- Step 5: Look up the precedence of the token on top of the stack
in the "Stack" column of the precedence table.
- Step 6: If the precedence of the top of the stack is greater than
or equal to the precedence of the input,
first pop the token off the top of the stack. If it is not a
"(", output it. Either way, go to Step 5.
Otherwise, if the precedence of the top of the stack is less
than the precedence of the input, then if the input token is
not a ")", push it onto the stack
- Step 7: Goto Step 1.
- Finished.
Infix to Postfix Example:5*(4-2+2)-6/3
Action: Initialize
Input: 5 * (4 - 2 + 2) - 6 / 3 )
Output: <empty>
Stack: (
Action: Read 5, output 5
Input: * (4 - 2 + 2) - 6 / 3 )
Output: 5
Stack: (
Action: Read *, push *
Input precedence: * = 3
Stack precedence: ( = 0
Input: (4 - 2 + 2) - 6 / 3 )
Output: 5
Stack: ( *
Action: Read (, push (
Input precedence: ( = 5
Stack precedence: * = 4
Input: 4 - 2 + 2) - 6 / 3 )
Output: 5
Stack: ( * (
Action: Read 4, output 4
Input: - 2 + 2) - 6 / 3 )
Output: 5 4
Stack: ( * (
Action: Read -, push -
Input precedence: - = 1
Stack precedence: ( = 0
Input: 2 + 2) - 6 / 3 )
Output: 5
Stack: ( * ( -
Action: Read 2, output 2
Input: + 2) - 6 / 3 )
Output: 5 4 2
Stack: ( * (
Action: Read +, pop -, output -
Input precedence: + = 1
Stack precedence: - = 2
Input: 2 ) - 6 / 3 )
Output: 5 4 2 -
Stack: ( * (
Action: push +
Input precedence: + = 1
Stack precedence: ( = 0
Input: 2 ) - 6 / 3 )
Output: 5 4 2 -
Stack: ( * ( +
Action: Read 2, output 2
Input: ) - 6 / 3 )
Output: 5 4 2 - 2
Stack: ( * ( +
Action: Read ), pop +, output +
Input precedence: ) = 0
Stack precedence: + = 2
Input: - 6 / 3 )
Output: 5 4 2 - 2 +
Stack: ( * (
Action: Pop (
Input precedence: ) = 0
Stack precedence: ( = 0
Input: - 6 / 3 )
Output: 5 4 2 - 2 +
Stack: ( *
Action: Read -, pop *, output *, push -
Input precedence: - = 1
Stack precedence: * = 4
Input: 6 / 3 )
Output: 5 4 2 - 2 + *
Stack: ( -
Action: Read 6, output 6
Input: / 3 )
Output: 5 4 2 - 2 + * 6
Stack: ( -
Action: Read /, push /
Input precedence: / = 3
Stack precedence: - = 2
Input: 3 )
Output: 5 4 2 - 2 + * 6
Stack: ( - /
Action: Read 3, output 3
Input: )
Output: 5 4 2 - 2 + * 6 3
Stack: ( - /
Action: Read ), pop /, output /
Input precedence: ) = 0
Stack precedence: / = 4
Input: <empty>
Output: 5 4 2 - 2 + * 6 /
Stack: ( -
Action: pop -, output -
Input precedence: ) = 0
Stack precedence: - = 2
Input: <empty>
Output: 5 4 2 - 2 + * 6 / -
Stack: (
Action: pop )
Input precedence: ) = 0
Stack precedence: ( = 0
Input: <empty>
Output: 5 4 2 - 2 + * 6 / -
Stack: <empty>
The stack is empty.
The input is empty.
We've terminated in a normal way; the output is the input
expresses as a postfix expression.
Back to LinkedLists
We've taken a little break from linked lists to explore what can be
done with stacks and queues -- each of whcih can be efficiently
implemented by the linked list we've developed so far -- one that
can insert and remove only at the head and tail.
But, now it is time to charge forward and explore a more powerful linked
list implementation -- we'll begin to operate in the middle of the list.
Inserting At Arbitrary Locations
One interesting task with linked lists is to insert at an arbitrary
location within the list. One simple case of this is a method to
insert a new item at a particular location within the list, e.g.
the 0th, 1st, 2nd, 3rd, 4th, ..., nth spots. We developed the
following code to do this during class:
public void insertAtPosition (Object newItem, int position)
throws IndexOutOfBoundsListException
{
// Error: Null item to insert
if (null == newItem)
throw new NullItemListException ("No item to insert");
// Error: Index is negative
if (0 > index)
throw new IndexOutOfBoundsListException
("Request index is negative -- list begins at 0");
// Special case: First item in list
if (0 == index)
{
head = new Node (newItem, head);
// Special case: Only item in list
if (null == tail)
tail = head;
return;
}
try // Make sure they didn't request an index beyond the tail
{
// Loop to find the right position
int index = 0;
Node indexNode = head;
while (index < (position-1))
index++, indexNode = indexNode.getNext();
// Insert the new item
indexNode.setNext(new Node (newItem, indexNode.getNext()));
// Special case: New last item of list
if (tail == indexNode)
tail = indexNode.getNext();
}
// Handle special case of index beyond end of list
catch (NullPointerException npe)
{
throw new IndexOutOfBoundsListException
("Requested position beyond end of list");
}
}
Another similar problem is to insert a new item in the list
after the first instance of some other item. We developed
the code below to solve this problem:
public void insertAfterFirstMatch (Object newItem, Object keyItem)
throws ItemNotFoundListException
{
// Error: Null item to insert
if (null == newItem)
throw new NullItemListException ("No item to insert");
// Error: Null key item
if (null == keyItem)
throw new NullItemListException ("Key item is null");
// Special case: First item in list
if (head.getData().equals(keyItem))
{
head = new Node (newItem, head);
// Special case: Only item in list
if (null == tail)
tail = head;
return;
}
try // Look out for the case where there is no matching item
{
// Loop to find the right position
Node indexNode = head;
while (!indexNode.getData().equals(keyItem))
indexNode = indexNode.getNext();
// Insert the new item
indexNode.setNext(new Node (newItem, indexNode.getNext()));
// Special case: New last item of list
if (tail == indexNode)
tail = indexNode.getNext();
}
// Handle special case of index beyond end of list
catch (NullPointerException npe)
{
throw new NoMatchingItemListException
("No item in list matches provided key");
}
}