Return to the Lecture Notes Index
15-111 Lecture 13 (Friday, Febrary 13, 2009)
Quick Sort: The Strategy
Although the sorts we've discussed so far have differed in the details,
they have all had the same basic strategy: Fill the sorted list in order,
one item at a time, by selecting the right element from the unsorted list.
Select this item by moving from one side of the unsorted list to the other,
making comparisons along the way.
We are now going to take a completely different approach. For the moment,
we need a small amount of magic. So, let me grant you a magic wand (Poof!).
If you point this magical wand at an unsorted list of numbers, it can, much
like a divining rod, find the "middle" number in the list. For example,
if we point it at the numbers
5, 7, 2, 1, 6, 8, 9
it will point at "6", the 3rd (starting with 0) number in the list -- the
middle one. This is a very powerful magic wand -- because we've now
found the right value for the 3rd position, and can just swap it into
place. We'll call this place the "pivot point", because it is right
in the middle of the list.
So, this magic wand makes sorting perfectly simple, right? We can just
zap some more numbers, right? Well, not exactly. We've got (at least) one
problem -- we've now got two lists, not one. The list to the left of the
pivot, and the list to the right of the pivot. Which one do we zap?
Well, we need to zap each of them, each has its own pivot point. But, there
is a problem with that, too. Each of the lists is unordered. Take a look
at the list again -- this time with the one pivot we know swapped into
place:
5, 7, 2, 6, 1, 8, 9
The list on the left has 7, which is greater than the pivot, and the list
on the right has 1, which is less than the pivot. 7 might be in the right
place, but these two lists don't have the right values.
So, let's start at the beginning of the left list and move right until
we find a value that should be in the right list -- 7. Then, let's start
at the right side of the right list, until we find a value that belongs
in the left list -- 1. Then, let's swap these two. We should repeat
this process, until everything in the left list is less than the pivot and
everything in the right list is greater than the pivot:
5, 1, 2, 6, 7, 8, 9
Now, we can just use that magic wand twice more -- once on the left list
and once on the right list. In fact, we are just going to do this recursively
until the list size is 2, at which time we'll just compare the two numbers,
and swap if necessary.
So, in the left list, we pick 2 as the pivot and swap it into place
5, 2, 1, 6, 7, 8, 9
Then, we swap the 1 and 5 with each other, since each is on the wrong side
of the pivot value, 2.
1, 2, 5, 6, 7, 8, 9
Now we repeat the same for the right list, selecting 8 as the pivot,
discoverign that it is in the right place, and then checking the values
in the left and right lists -- each of whcih contains one number that
is in the right place:
1, 2, 5, 6, 7, 8, 9
Now, we repeat this, again recursively on each of the sublists. But, we
discover that each has a length of 1, so we know that each is in the right
place (how to get a list of one to be out of order?)
Think about what we're doing here, we're dividing thi list in half, and
then half again, and again, until the list has only one item. For this
reason, Quicksort is often known as a divide adn conquer algorithm.
By using recursion, we cave the problem into smaller and smaller pieces,
each of which is much easier to solve.
1, 2, 5, 6, 7, 8, 9
Quick Sort: Making the Magic Disappear (Poof!)
So, given this magic wand, we can sort a list. Pretty cool, huh? But, what
about without this magic wand? Easy answer -- we just pretend. We pick
a value, and pretend it is the pivot. If we are right, the sort proceeds
as we've discussed. If we aren't right, no big deal -- the left and
right lists will just be different sizes. This is suboptimal, but still
functional. The only problem is that we have learned less about the positions
of the numbers than we otherwise could. Imagine if we'd pick the lowest
(or highest) number in the list as the pivot. We'd still put it into its
place -- but all of the vlaue would be on one side of it. We wouldn't be
able to divide the problem at all.
At the implementation level, to facilitate things, weh we guess at the
pivot, we are going to swap it out of the list, into the last element,
to get it out of the way. Unlike our magically perfect pivot value,
we don't know exactly where it goes, until we divide the list into
those things that are less than it and those things that are greater than
it. At that point, we know where the two lists meet, and can swap the
pivot value into the proper place.
Which number do we guess is the pivot? Well, since we don't know, if the
unsorted list was truely in a random order, we could pick any -- the first,
the last, or anything in between -- we'd have an equal change of being
right -- and no greater a chance of being more wrong. But, if the list
doesn't happen to be in a random order, there are better and worse choices.
For example, if the list is sorted, and we always pick the first value,
it will always be the worst choice -- everything will be greater than it.
The same is true if we always pick the alst value and the list is sorted
the opposite way. We could pick a random value each time -- just pull
a number out of the hat, per se. And this will prevent a consistently
bad choice -- but it'll waste some time picking a random number and could
still be bad, sometimes.
So, instead, we'll take the number in the middle of the list. If the list
is in a random order, it is as good as any. But, if the list is in sorted
order, whether forward or backward, it is optimal. The middle value will
be in the middle. Of course, there is still a worst case ordering for
this approach -- but it is somewhat less likely given human behavior.
Quick Sort: A Real Example
Let's take a look at quicksort in a more structured example. This time,
we're going to pick the middle value as the pivot. And, we're going to swap
it out of the list, until we divide the list into two sublists, each
of which has either vlaue less than the pivot, or greater than the pivot.
Once we do that, where the two lists meet is the pivot point, so we can
swap it into its proper place.
This is the initial state of our quicksort example (sorted elements are italicized).
| 5 |
8 |
1 |
4 |
3 |
7 |
6 |
9 |
11 |
10 |
12 |
2 |
After sorting the rest of the list based on if it's in the right place relative to the pivot,
we find that the pivot should be where the 8 now is.
| 5 |
6 |
1 |
4 |
3 |
2 |
8 |
9 |
11 |
10 |
12 |
7 |
So you swap them and QuickSort is then recursively called on the first half of the
sequence up to the old pivot, with 4 as the new pivot,
up unto the pivot.
| 5 |
6 |
1 |
4 |
3 |
2 |
7 |
9 |
11 |
10 |
12 |
8 |
The 4 gets swapped with the 2, which is the last element of the partition, and all the elements
are tested to see if they belong in the right place, and it's determined that in the lower array, where the 6 is, is
where the 4 should be.
| 3 |
2 |
1 |
6 |
5 |
4 |
7 |
9 |
11 |
10 |
12 |
8 |
Now the 4 is in place, so the 2 is the new pivot of that lower partition.
| 3 |
2 |
1 |
4 |
5 |
6 |
7 |
9 |
11 |
10 |
12 |
8 |
The 1 and 3 get swapped because they're in the right place, and the two gets put back.
Since the partitions are each one element big, we know they're done.
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
11 |
10 |
12 |
8 |
The six becomes the next pivot for the next sub-array, and since it's in the right place,
that's done too. So now we look at the upper partition from placing the first pivot in its spot.
First we choose the the 10 as the pivot.
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
11 |
10 |
12 |
8 |
We switch it with the 8, which is at the end, and check the elements to see if they're on the
correct sides. We end up having to swap the 11 and the 8. So now we know where the 10 goes, and we swap
with the 11.
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
8 |
11 |
12 |
10 |
We switch it with the 8, which is at the end, and check the elements to see if they're on the
correct sides. We end up having to swap the 11 and the 8. So now we know where the 10 goes, and we swap
with the 11.
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
8 |
10 |
12 |
11 |
After doing the same recursive calls on the two-element partitions, we have our ordered list.
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Quick Sort Code
/*
*quickSort() calls sortPartition()
*/
public void quickSort(int[] numbers)
{
sortPartition (0, numbers.length-1);
}
/*
* This is a helper method which is used by findPartition() to
* find the "pivot point" - the place to divide the partition.
*/
private int findPivot (int left, int right)
{
return ((right + left)/2);
}
/*
* This is a helper method called by sortNumbers(). It sorts
* an individual partition about the given pivot point.
*/
private int partition (int left, int right, int pivot)
{
do
{
while (numbers[++left] < numbers[pivot]);
while ((right !=0) && (numbers[--right] > numbers[pivot]));
swapNumbers (left, right);
} while (left < right);
swapNumbers (left, right);
return left;
}
/*
* This is a helper method called by sortNumbers(). It recursively
* calls itself on subpartitions to sort the numbers. The actual
* sorting within the partition is done by sortPartition(), which
* is iterative.
*/
private void sortPartition (int left, int right)
{
int pivot = findPivot (left, right);
swapNumbers (pivot, right);
int newpivot= partition (left-1, right, right);
swapNumbers (newpivot, right);
if ((newpivot-left) > 1) sortPartition (left, newpivot-1));
if ((right - newpivot) > 1) sortPartition (newpivot+1, right));
}
Big-O: Quick Sort, Magical Version
The best, average, and worst cases of quicksort actually turn out to be very
different, because of the variabilitity introduced by the choice of
pivots.
If we view Quick Sort in the magical/ideal case, we see that the we end up with
a recursive tree that is O(log n) deep and does O(n) work at each level
for an overall complexity of O(n log n).
The reason that, in this magical/ideal case, the recursive tree is O(log n)
deep is that each recursive call divides the list in half and makes recursive
calls for each half. We can only divide the list log-n times, before we end up
with partitions of size=1.
It is also interesting to observe that, at each level of recursion, the total
amount of work is constant. Each activation of the quick sort function at
the same level processes a partion that is independent (non-overlapping)
of the others. If we assume that some level has p partitions,
each partition, contains, neglecting the absence of the pivot,
n/p items. So, across a single level, we've got approximately
n=(n/p)*p work. Thus, our sort, as a whole requires
log n levels * n work/level work. Thus, in the optimal case,
Quick Sort is O(n log n).
Consider the following figure:

Big-O: Quick Sort, The Real Version
Of course, the Big-O of Quick Sort isn't O(n log n), because we can't
magically pick the correct pivot each time. So, let's figure out the real
Big-O. How does it behave in the worst case?
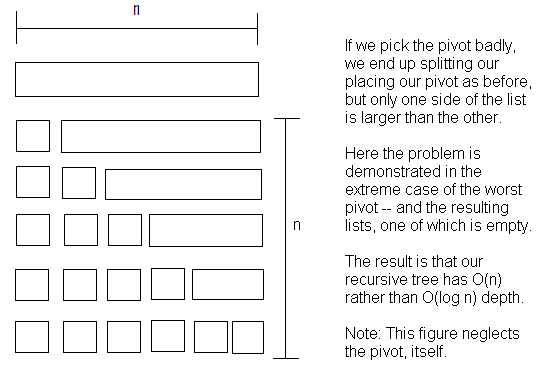
Well, if at each opportunity we pick the worst pivot, this means that
one of the two "halfs" is actually empty -- all of the items are in the
other partition. The consequence of this is that our recursive tree can
become O(n) deep. None-the-less, each level still has O(n) work to do.
We end up with a perofmrance of O(n2) as shown below:
In this respect, a worst-case quick sort is much like a bubble or selection
sort. But, as it turns out, either is more efficient than a worst-case
quicksort. The reason is that quicksort uses recursion, which is quite
expensive -- even more expensive than bubble sort's constant swapping.
So, if the pivot is bad, there is very little algorithmic gain -- but
a lot of additional overhead.
The same is actually true for small lists, even in the optimal case --
the overhead of recursion outweights the algorithmic gain for small
lists. So, in truth, it doesn't make sense to quicksort down to a list
size of 1 or two. A more typical strategy is to quick sort down to a
list size of 50-100, and then use a selection sort.
Quick Sort and Big-O: What Gives?
If Quick Sort is O(n2), why would anyone use it? And, why
do they call it quick? In the average case, empirical analysis has shown
performance to be much closer to optimal than worst case -- still N*Log N.
The reality is that, as long as we pick the pivot sensible, e.g. middle or
random, and our data isn't intentionally designed to be toxic, the performance
can reasonably expected, in practice, to require c*(n log n) runtime.

