Slides4

Lecture #4

Chapter 12 (even though homeworks emphasize
stoichiometry practice still)

CURMUDGEON GENERAL'S WARNING. These "slides" represent highlights from lecture and are neither complete nor meant to replace lecture. It is advised not to use these as a reliable means to replace missed lecture material. Do so at risk to healthy academic performance in 09-105.

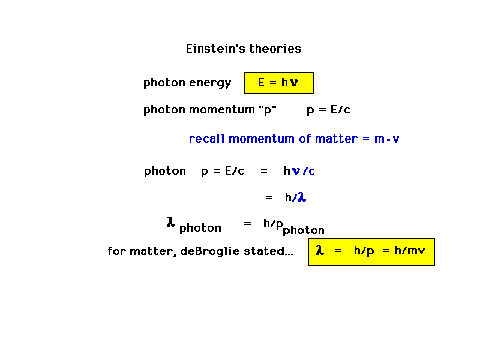
DeBroglie's hypothesis of wave-particle duality. This will lead us to the current theories.

The wavelength associated with everyday matter (a baseball) is so small, we don't see the effects of wave-particle duality. Here, we see how the wavelength depends on the total energy and the forces acting on a particle, the latter showing up as potential energy (which can vary with position of a particle in space).

The next step was to take the equation for describing how the amplitude of light varies in space (equation not given yet) and convert it into an equation that shows how a particle's wave amplitude varies in space. This is done by using deBroglie's wave length for matter. We then get a wave equation for matter.

Lecture Outline

(New Quantum Theory)

Particle-in-a-box model

one dimension

two dimenstions

three dimensions

Schrodinger's Wave Equation applied to the hydrogen atom

n, principal quantum number

l, angular momentum or shape quantum number

m_l, magnetic or orientation quantum number

Electron "spin"

m_s, spin quantum number

Energies and geometries

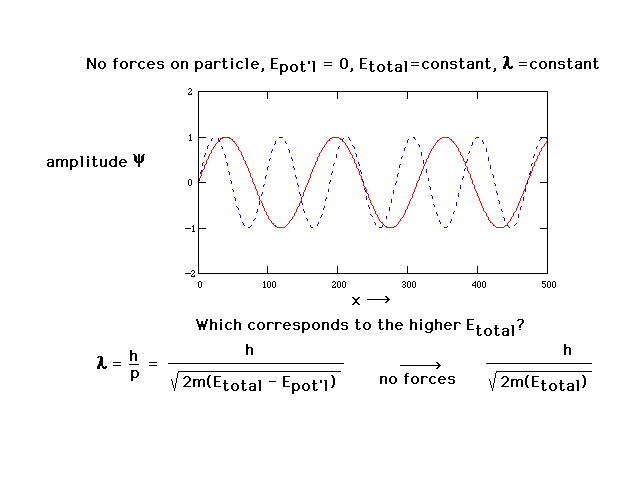
With no forces present and total energy constant, the wavelength is constant. This is now just a sine wave. The amplitudes of two such sine waves are shown here. The amplitude of a wave function has no physical significance but will allow us to determine two features of systems that we do have an interest in: geometry and energy (of electron distributions in atoms and molecules).

The particle-in-a-box model (Section 12.6 in the text), a very simple demonstration of wave behavior of matter. We will need to understand this model for 09-105.

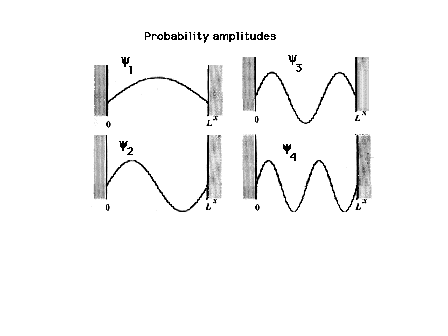
Levels 1 through 4 for a particle in a box; the wave functions or probability amplitudes must be zero at the walls of the box. This restricts the sinusoidal choices.

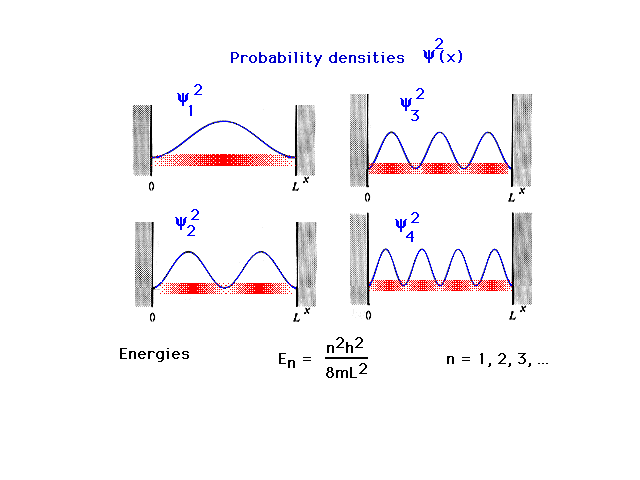
The density distributions or probability densities for the quantum mechanical particle-in-a-box are shown. These are determined from the squares of the amplitudes. The allowed energies of the particle follow a simple formula involving an integral "quantum number", n. These discrete energies are the only ones that exist for this simple system. (The formula will always be given to you. There is no need to memorize it for 09-105.) The blurred density distributions tell you where you are likely or unlikely to find the particle in each of the energy states shown.

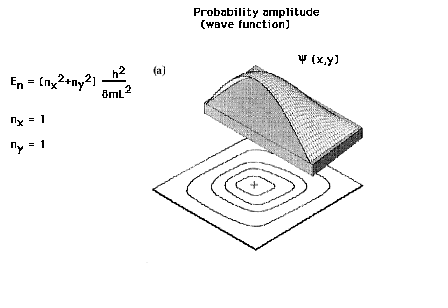
The particle in a two-dimensional box

The lowest energy state for the particle in a two-dimensional box is describe by two integral quantum numbers.

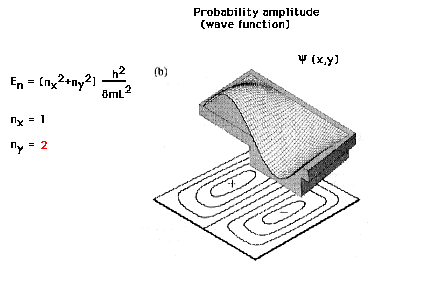
Wave function for the first excited state of the particle in a 2D box

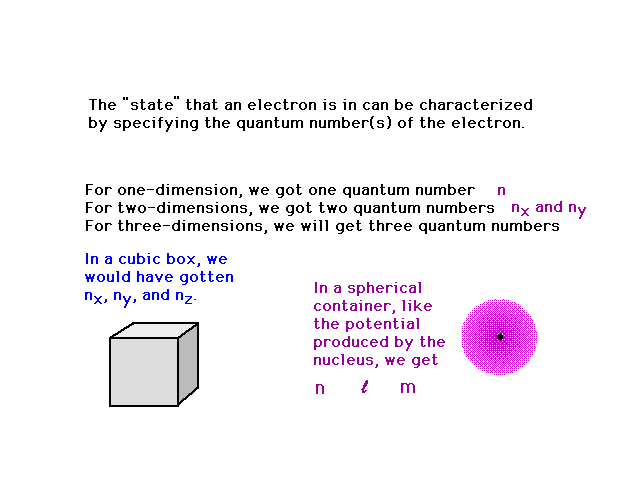
We could go to a cubic three dimensional system getting three quantum numbers (n_x, n_y and n_z). But let's jump right to the hydrogen atom in which the electron moves in a spherical well (produced by the central nucleus' positive charge).

The principal quantum number, n, determines the total energy of the electron

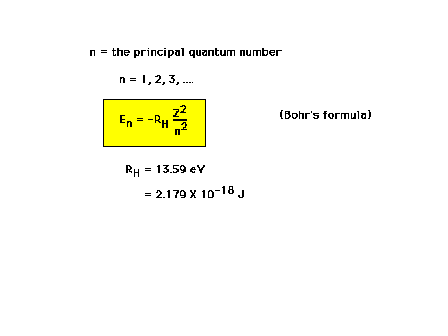The angular momentum quantum number will determine the three dimensional shape of the wave function, how it is distributed about the mathematical origin. Restrictions on the allowed values of this quantum number arise from the mathematics (which we don't look at in this course).

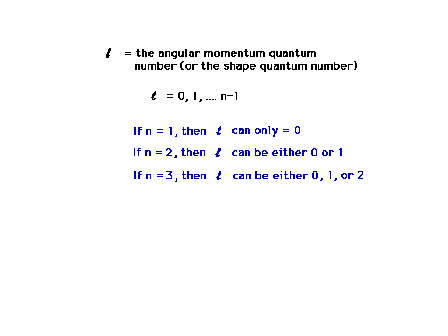There is an alternative set of symbols representing the various angular momentum states of an electron.

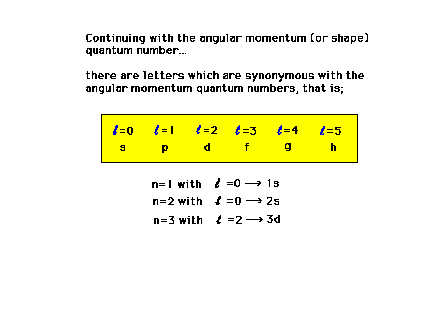The "size" of the region of space occupied by an electron is difficult to quantify. The average size depends mostly on n and to a lesser extent on the angular momentum quantum number, l. (You do not need to know this equation.) The essence of this relationship is very well captured by Bohr's original formula for the radii of his planetary orbits, r_n = a_on²/Z.

The third quantum number is the magnetic quantum number and refers to the behavior of an electron in an atom if a magnetic field were present as well. Later (when we're looking at pictures), we will find it also indicates the orientation in which the wave distribution points.
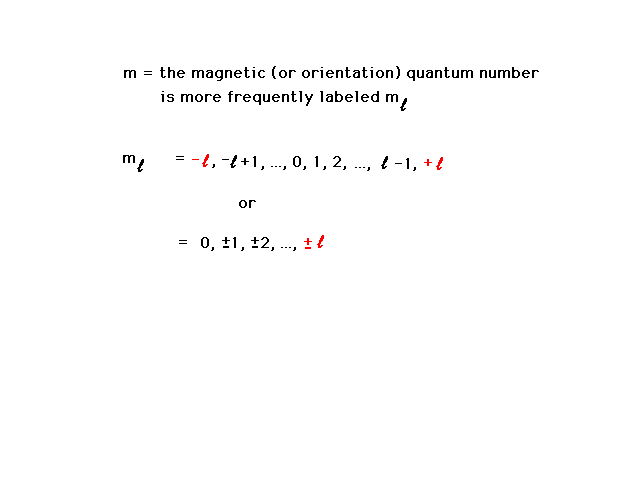