| Lecture #32 | ||
Text: Chapter 19, sections 4 and 6. |
|
|
| Lecture outline | Transition metal complexes
|
|
| A class of isomers called "stereoisomers" consists of geometrical isomers, which we already have seen examples of, and "optical isomers", also called "enantiomers". Optical isomers are said to be "chiral" and have a distinction between them that is similar to the distinction between the left hand and the right hand. |  |
|
| A tetrahedral arrangement symbolized as Mabcd (four
different ligands) consists of two possible optical
isomers.
|
 |
|
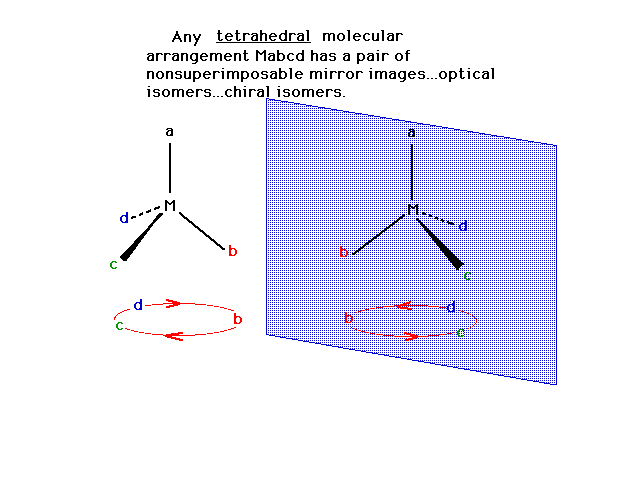| The octahedral arrangement symbolized by Ma2b2c2 where the three pairs of ligands are all "cis" with respect to each other has two optical isomers. |  |
|
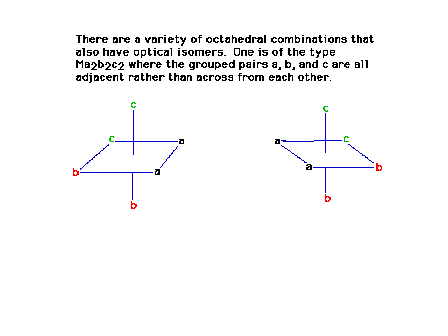| The previous structure rotated so as to match up the ligand pairs b and b with that of the mirror image, also matching up one of the a ligands. The two structures are not superimposible meaning that they then must be optical isomers. |  |
|
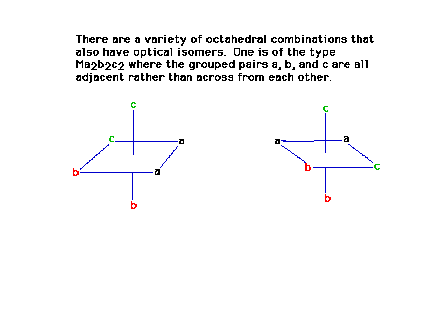| The octahedral complex Ma2b2c2 in which the ligands are all "trans" to each other is a geometrical isomer of the "cis" arrangement. Its mirror image will be superimposible and therefore there are no optical isomers of this structure. |  |
|
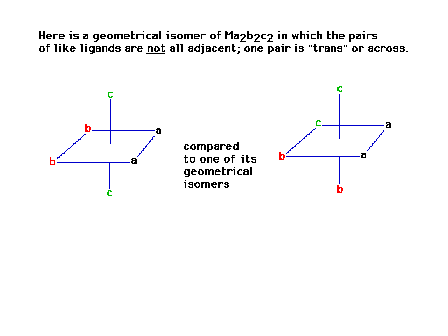| The mirror image of the previous complex |  |
|
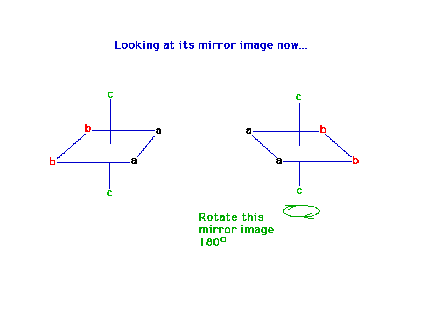| The two structures (original + mirror image) are identical. |  |
|
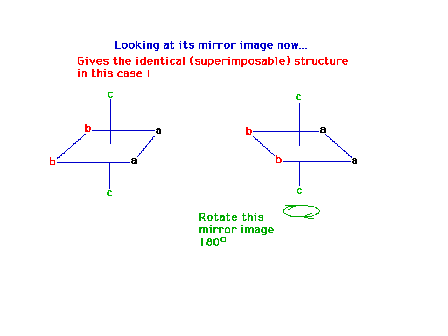| The electron configuration of the transition metal ion Co3+ |  |
|
| Light absorption properties of some Co3+ complex ions |  |
|
| Magnetic properties of some Co3+ ions |  |
|
| Geometrical properties of some transition metal ions. |  |
|
| Crystal field theory addresses all the "puzzles" from the previous lecture. |  |
|
| Developing the idea of crystal field theory.. |  |
|
 |
||
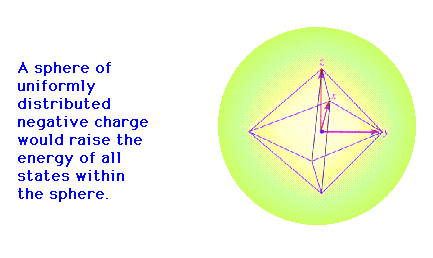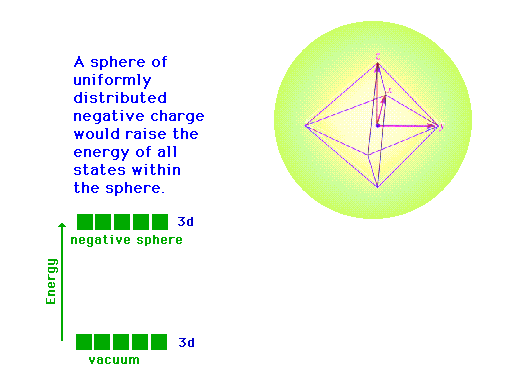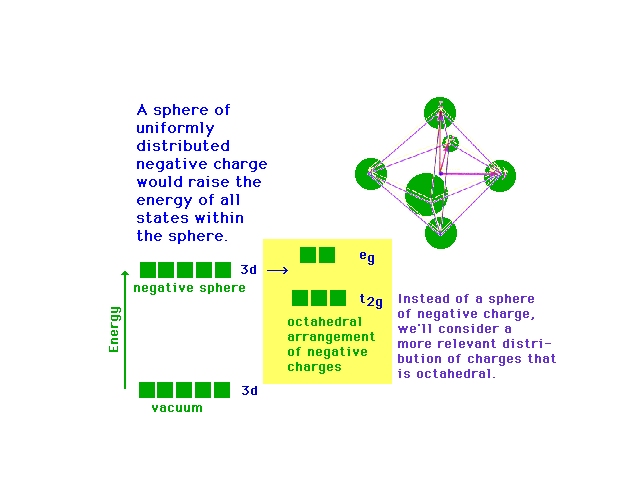
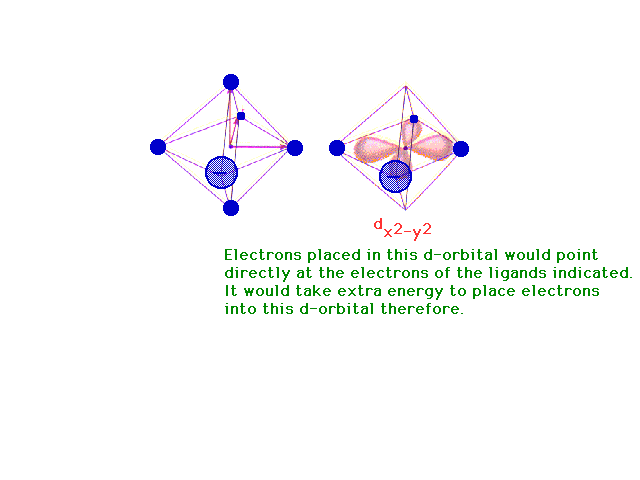
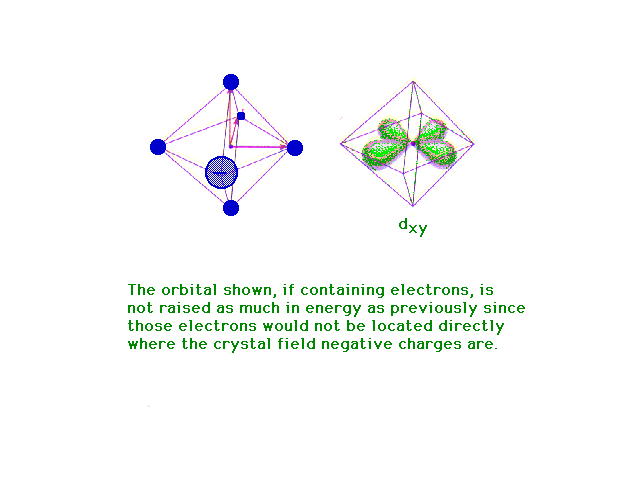
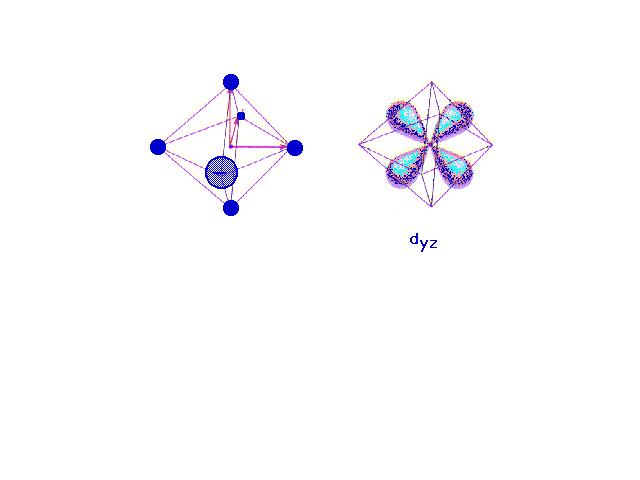
| Following what happens to the outer d-orbitals when a transition metal ion is placed in a spherically distributed negative charge, and then one that has octahedrally deployed negative charges. |  |
|
 |
||
 |
||
 |
||
 |
||
 |
||
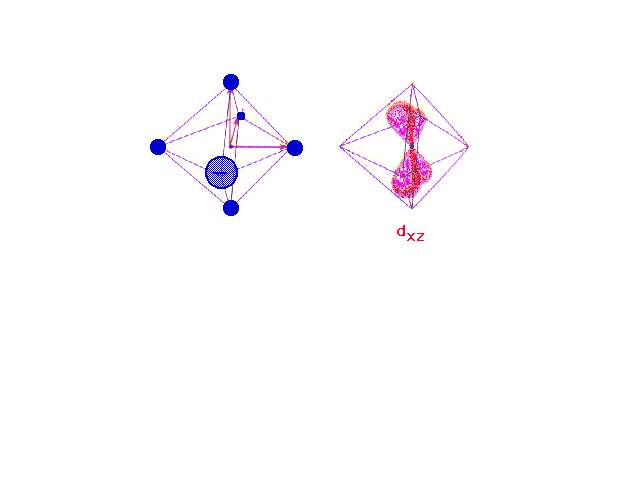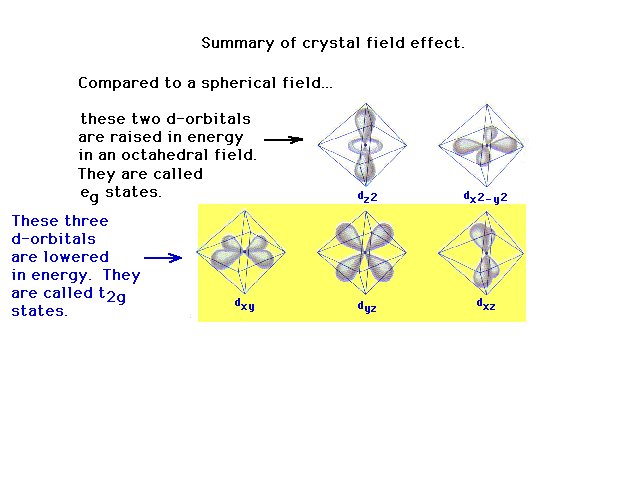| The weak field splitting and strong field splitting of the d-orbitals illustrated. |  |
|
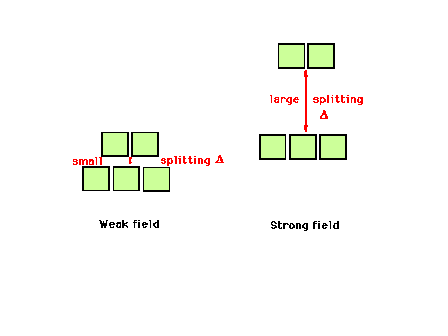| You need to know the relative crystal field strengths of a restricted number of ligands indicated here. |  |
|
| The electron configuration in the weak field complex CoF63- and the strong field complex Co(NH3)63+. |  |
|
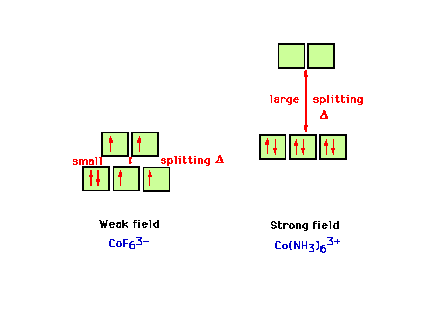| Co3+ complex ions, their crystal field splitting energies, the color of light absorbed, and the color that the complex appears. |  |
|
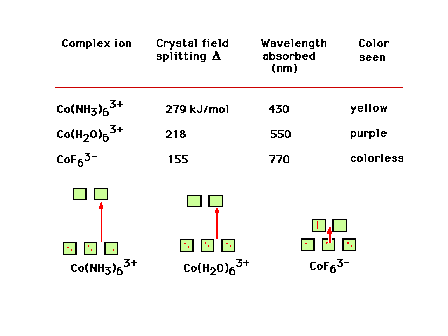| Leaving the discussion of coordination number = 6 (octahedral geometries) and proceeding to coordination number four. |  |
|
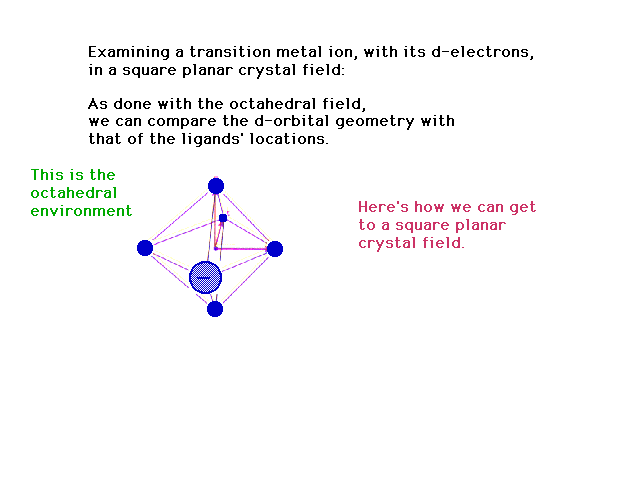
| Changing an octahedral geometry into a square planar geometry distribution of charges |  |
|
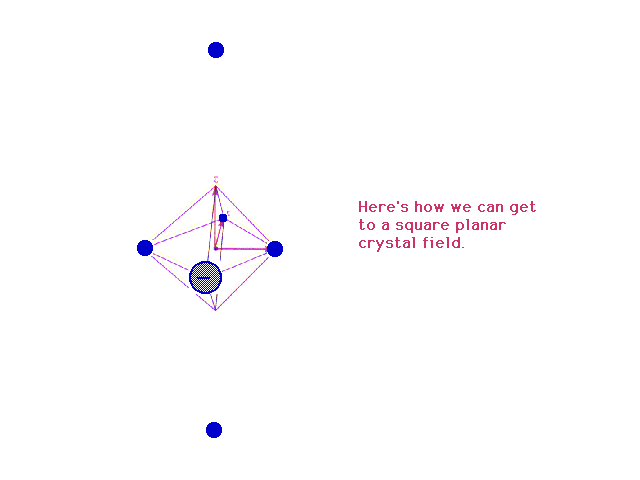
| Removing the ligands (charges) along the z-axis to an infinite distance from the central species converts the octahedral geometry to a square planar geometry. |  |
|
| What kind of change to we expect the removal of z-axis charges to have on the 3d valence orbitals? |  |
|
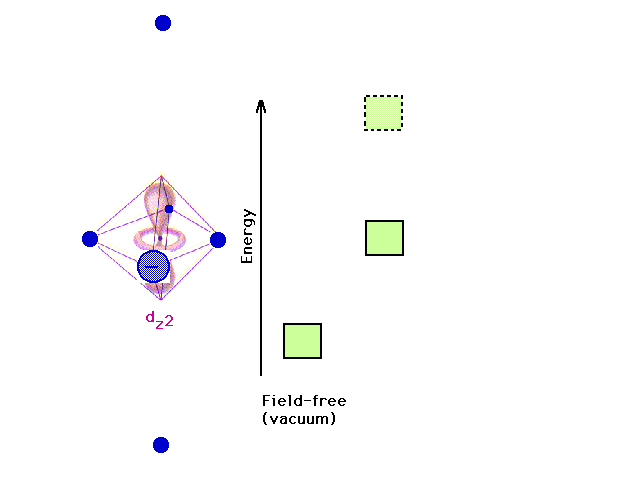
| Removing the z-axis ligands stabilizes the dz2 orbital relative to its previous energy. |  |
|
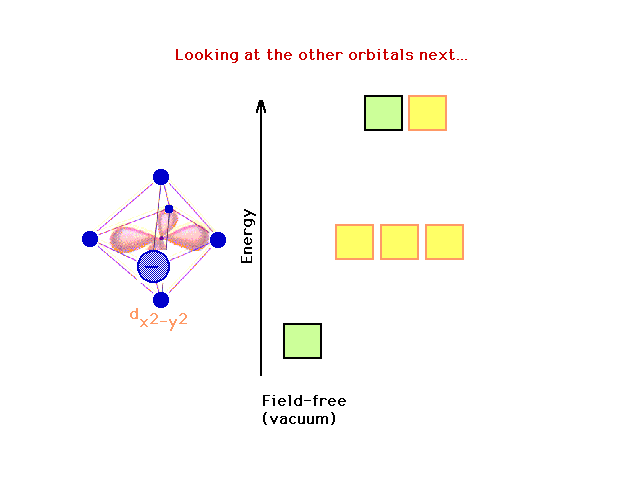
| How are the remaining d-orbitals (shown in yellow) affected by removing the z-axis charges? |  |
|
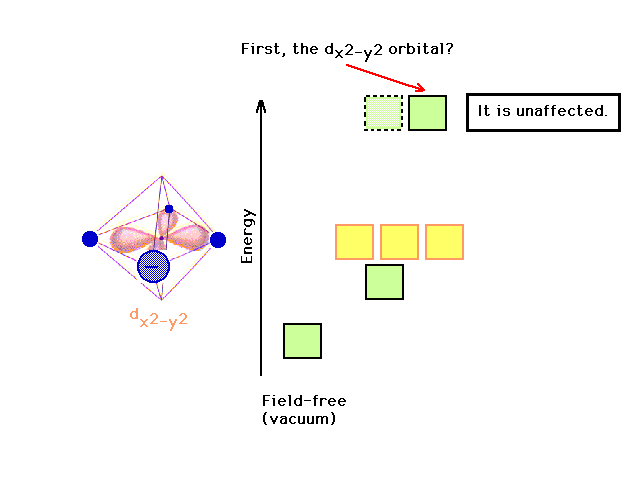
| Although the dz2 has been stabilized (lowered in energy), there is no effect on the dx2-y2 orbital in changing something along the z-axis. |  |
|
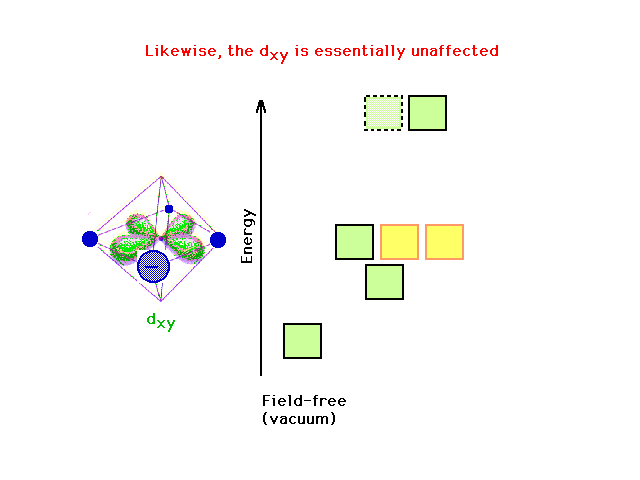
| There is also no effect on the dxy orbital energy (now shown in green) of changing the charge on the z-axis. |  |
|
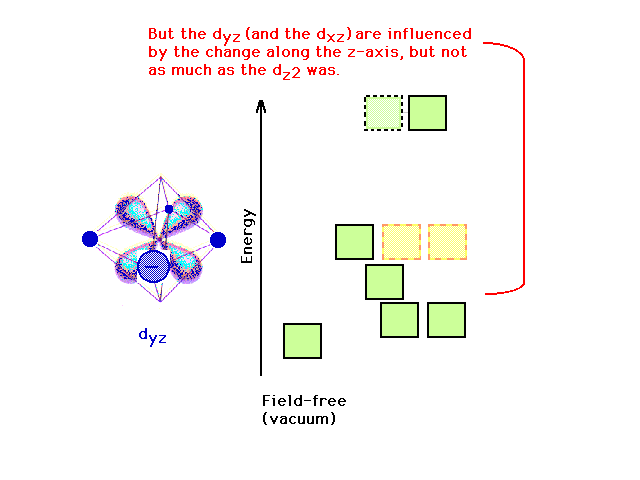
| Both the dxz and dyz are lowered in energy (become stabilized) when charge along the z-axis is removed. |  |
|
| Summary of the switch to a square planar geometry |  |
|
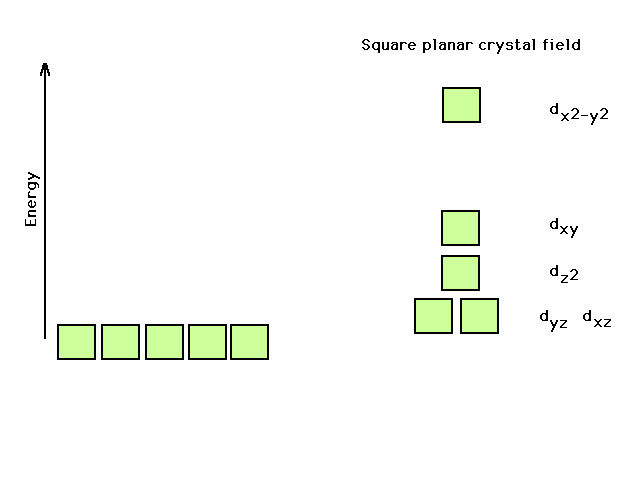
| The valence electron energy diagram for d-electrons in a square planar geometry (crystal field). |  |
|
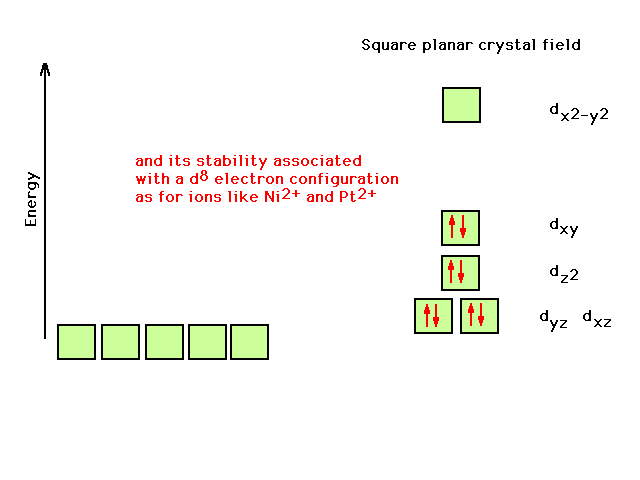
| Now it becomes clear that the square planar geometry correlates with the observation of extra stability of a transition metal comlex ion with a d8 configuration on the central atom |  |
|
