Hybrid Atomic Orbitals 
|
|
Please send questions
and/or comments to the course bboard
or to PK03 to help make this particular add-on more
useful.
|
|
For those who are interested, we'll attempt to give a
slightly deeper explanation of what hybrid orbitals are
in the context of wave behavior.
|
|
We'll use the hydrogen
atom in its ground electronic state as a way to start the
discussion.
|
|
It shouldn't be surprising
that the discussion is based on the premise that wave
behavior underlies the description of where electrons are
expected to be found and what energies they might have.
|
|

This is the 1s "pure" atomic orbital. |
The (electronic) ground state of an
isolated hydrogen atom is intimately familiar to you. At
least at some level; certainly pictorial. The electron is
subject to the spherically symmetric electrostatic
attraction to the positive nucleus. (That is, all
directions out from the nucleus map the same
electrostatic force acting on an electron.) Putting such
an arrangement into the (Schrödinger) wave equation
gives an infinite number of allowed solutions...wave
functions and their associated energy values. The ground
state is the familiar spherical shape.
|
Suppose we had a hydrogen atom next to
a hypothetical positively charged plate (shown as blue) and were interested in the ground electronic
state in this situation. The wave equation would
incorporate the forces acting on the electron -- the
attraction to the nucleus and the attraction to the
positive plate. The resulting wave function for the
ground state would look qualitatively as indicated to the
right.
|
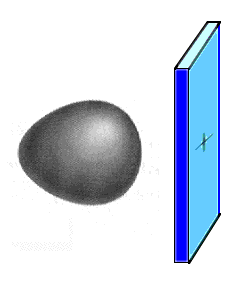
This is the ground state atomic orbital for an
electron held strongly to the hydrogen nucleus, yet
affected by a second nearby positive charge. |
How do we describe the
electron's ground state atomic orbital here? It turns out
that the exact answer (pictured) can be very closely
approximated by saying that if you took a simple mixture
of wave functions you already know, perhaps 90% 1s and
10% 2pz, the combination would look almost
perfectly like the true answer. That combination is like
breeding a hybrid from mixed parentage... and the
approximate result is referred to as a hybrid atomic orbital. It would appear nearly
identical to what is already displayed as the exactly
correct result, but now we can talk about it using
existing vocabulary (although giving it a name in this
example would be awkward).
|
|
Now about atoms in complex
chemical structures. When a carbon atom with its 2s and
2p valence orbitals (four valence electrons in all) about
the carbon nucleus (plus inner core electrons) is moved
into an atomic environment that has two additional
positive charges arranged in a linear fashion with carbon
at the center, the wave equation no longer produces pure
2s and 2p atomic orbitals, but rather orbitals that look
very much like what you get by taking 50:50 mixtures
(that is, equal parts) of the 2s and 2pz
(leaving the other two 2p's almost unaltered). The
mixture, being equal part s and p, is abbreviated an
"sp" orbital, so we have a name for it. One
mixture adds 2s+2p and the other subtracts (2s-2p). Each
of these mixtures is again a hybrid atomic orbital, very
closely approximating the exact result. Each such hybrid
orbital can contain up to two electrons.
|
|
 |
These are the pure 2s (left) and
pure 2p (right) atomic orbitals that would be expected if
carbon (or any other atom or ion) were under
consideration.
|
The above pictures
representing visualizations of the 2s and 2p wave
functions would be incorrect if the attraction of
electrons were from other than a single, centrally
located nucleus. We'll consider a simple pictorial
example below.
|
|
 |
 |
These two illustrations have placed
the carbon atom between two positive charges (which could
be other nuclei or atoms with affinities for drawing
electrons). These are two equal energy hybrid
solutions that can be synthesized by adding and
subtracting, respectively, the previous pure
atomic orbitals on the central atom. In this one, the
electron distribution around the carbon is pulled toward
the right positive charge. (In this arrangement, the
remaining two valence orbitals are barely changed from
their original description, pure 2p's (since they are not
directed at the perturbing electrostatic forces). For
convenience, they are considered to remain pure atomic
orbitals.
|
In this hybrid combination, the
electron distribution is pulled toward the left positive
charge. |
| In summary, depending on
the environment around valence electrons of an atom,
different wave forms are generated by quantum mechanics.
The directional character of these revised atomic
orbitals is determined by the symmetry with which the
perturbing forces are geometrically distributed around
the originally isolated atom. Here we have looked at just
a linear geometry of external influences on the valence
electrons. In class, we look at trigonal planar,
tetrahedral, trigonal bipyramidal, and octahedral
environments as well. A tetrahedrally dispersed geometric
arrangement about an atom would necessitate that the s
and all three p valence orbitals be abandoned and
be replaced instead by four new orbitals. These four
valence orbitals are very closely mimicked by hybrids
that are each one part s and three parts p; that is, each
is a sp3 hybrid atomic orbital. Other sites: 4
|
|
![]()