Section 1.01       Biochemistry I, Fall Term                                                                                           Sept 2, 2005

 

Lecture 3:  Acid-Base Equilibria & Buffers

Reading in Campbell:  Chapter 2.3-2.6

Key Terms:                                                                  

 

3.1 Acids and Bases and Acid Strength

 

Example:

 

 

 

 

 

 

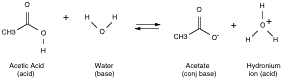
Acid strength:

A compound is an acid if it loses its proton, and it is a base if it takes up a proton.  For a simple acid like X-H, acid strength depends on the strength of the X-H bond and the stability of the charged anion X-.  Weaker bonds generally lead to greater acidity.

H2O < H2S < H2Se

HF < HCl < HBr  

                                                                                         

 

HF > H2O

HCl > H2S

 

 

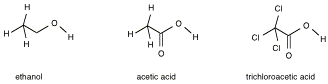Consider the following three compounds:

 

 

 

 

 

 

 

 

 

The negative charge on the ionized acid can be further stabilized by resonance structures that distribute the negative charge as well as by nearby electron withdrawing groups.  The nearby presence of formal positive and negative charges also affects acidity.

3.2 General Equilibrium Reactions:

 

Consider first a very simple reaction and its equilibrium features: 

                 

 

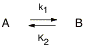
The following rate equations can be used to describe the reaction:

 

                  

 

At equilibrium there is no change in the concentration of A or B, therefore:

 

                                   

 

At equilibrium the reaction has not stopped, but rather, the rates of the forward reaction (k1[A]) and the reverse reaction (k2[B]) are equal.  Thus:

 

                                   

 

 

3.3 Ionization of H2O and definition of pH:

 

 

The equilibrium constant for the dissociation of H2O can be written:

                              

Since the concentration of H2O is high (55.5 M) and practically constant, we can incorporate it into the equilibrium constant and define a dissociation constant for H2O:

 

 

Pure H2O is neutral.  Therefore ionization produces equal concentrations of H+ and OH-, and

 

                                                     

 

There is a reciprocal relationship between [H+] and [OH-].  In solutions that are acidic, [H+] is high and [OH-] is low.  Conversely, in solutions that are alkaline, [H+] is low and [OH-] is high.  Note that the ion product is always .

 

pH Definition:  pH is measured as the .  The lower the pH, the more acidic the solution.  Neutral pH is 7.0.  At this pH there are an equal number of H+ and OH- ions in solution.

Relation of [H+] to [OH-] to pH

pH

 

[H+], M

 

[OH-], M

0

 

100

 

10-14

1

2

3

 

10-1

10-2

10-3

 

10-13

10-12

10-11

4

 

10-4

 

10-10

5

6

 

10-5

10-6

 

10-9

10-8

7

8

 

10-7

10-8

 

10-7

10-6

9

10

11

12

13

14

 

10-9

10-10

10-11

10-12

10-13

10-14

 

10-5

10-4

10-3

10-2

10-1

100

 

--- Hydrochloric Acid (1 M)

 

--- Human gastric contents

 

--- Tomato juice

 

--- Cow¹s milk

--- Human blood plasma

--- Human pancreatic juice

 

 

--- Ammonia (1 M)

 

 

--- Sodium hydroxide (1 M)

 

 

3.4 Characterization of Acid Strength using pKa.

 

When an acid HA is added to H2O,

 

                                                       

 

The equilibrium constant for its dissociation is defined:

 

                                                     

 

                                                     

 

The acidity constant, Ka, is a fundamental property of the acid and does not depend on the pH of the solution.  Stronger acids have larger Ka values since they are more fully dissociated.

 

The Henderson-Hasselbalch Equation:  Since the proton concentration is always measured in units of pH, it is useful to modify the above equation by taking the negative log·:

 

                                   

 

which gives rise to the Henderson-Hasselbalch equation:

                 

 

 

 

The pKa is the ­log Ka.  Therefore strong acids have small pKa values.

 

Monoprotic acids (release only one proton):

Acid

 

 pKa

                              Type

HCl

 

-7

                     Very strong

Acetic Acid

 

4.76

                     Weak

Ammonium (NH4+)

 

9.25

                     Very weak

Methanol

 

16

                     Extremely weak

 

 

 

 

 

3.5 Solving pH Problems:

 

The H&H equation has predictive value.  Once you know the pKa of an acid and the pH, you can predict [A-]/[HA].  One particular case is routinely used in biochemistry: Given a pH and pKa of an acid, calculate the fraction of the acid that is protonated: fHA = ([HA]/AT) and the fraction that is deprotonated:

fA- = ([A-]/AT), where AT is the total concentration of acid: AT = [HA] + [A-].

 

 

Defining R = [A-]/[HA]

                  pH = pKa + log([A-]/[HA])

                  pH = pKa + log(R)

pH ­ pKa = log(R)

10(pH-pKa) = R

 

Once R is found, the fraction protonated and

deprotonated is obtained as follows:

 

[A-]/[HA] = R

                  [A-] = [HA]R

                  [AT] = [A-] + [HA]

                  [AT] = [HA](1+R)

 

 

Using the ionization of the side chain of the amino acid Histidine as an example (pKa = 6.0)

           

pH

                         (i)    R

FHA

4

5

R = 10(4-6) = 10-2

R = 10(5-6) = 10-1

FHA = 1/(1+0.01)= 0.99

FHA = 1/(1+0.1) = 0.91

6

R = 10(6-6) = 100

FHA = 1/(1+1) = 0.5

7

R = 10(7-6) = 101

FHA = 1/(1+10) = 0.091

8

R = 10(8-6) = 101

FHA = 1/(1+100) = 0.01

 

There are four general statements that are useful to remember:

1.     When the pH = pKa, [HA] = [A-].

2.     When the pH is lower than the pKa, [HA] > [A-].

3.     When the pH is higher than the pKa, [HA] < [A-].

4.     A pH change of 1 leads to a 10 fold change in the ratio of [A-]/[HA].

 

3.6 Titration Curves

 

Ka values are usually measured by direct experiment, usually with a pH titration.  Known amounts of a strong base (NaOH) are added to a solution of a weak acid and the pH is measured as the amount of NaOH is added.  As the base is added it removes the proton from the acid, as well as increasing the pH.

 

Inflection point (pH = pKa):  You can prove from the Henderson-Hasselbalch equation that the smallest change in pH due to addition of base occurs when the pH = pKa; at this inflection point, the pH of the solution is the pKa of the acid.

 

Equivalents:  moles of base/moles of acid, the x-axis for titrations.  Varies from 0 to 1 for monoprotic acids.

 

Equivalence point:  Complete deprotonation of the weak acid occurs when the molar amount of base is equal to, or equivalent to, the molar amount of weak acid.  This point in the titration is referred to as the equivalence point.

 

Example titration curve:

 

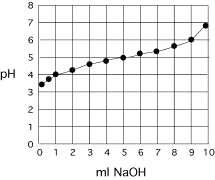ml NaOH                 measured pH

 

0.25                          3.20

0.5                             3.80

1                                 4.07

2                                 4.44

3                                 4.62

4                                 4.87

5                                 4.96

6                                 5.17

7                                 5.33

8                                 5.64

9                                 5.96

10                              7.00

 

 

 

Facts:     Concentration of NaOH = 1 M

                  Volume of solution that is titrated = 100 ml

 

Possible acids (from Campbell table 2.6)

                  Pyruvate                pKa = 2.5

                  Acetic Acid           pKa = 4.8

                  Tris                            pKa = 8.3

 

Questions:

1.              What is the pKa of the acid?

2.              Which acid is it?

3.              Give the x-axis scale in equivalents.


· Remember that pX is the negative log of X: e.g. pH = -log[H+].

 Also recall that log(ab) = log a + log b and log(a/b) = log a ­ log b.